What is CSC function in Excel?
The CSC function is one of the math functions of Excel.
It returns the cosecant of an angle.
We can find CSC function in Math&trig of insert function Tab.
How to use CSC function in excel
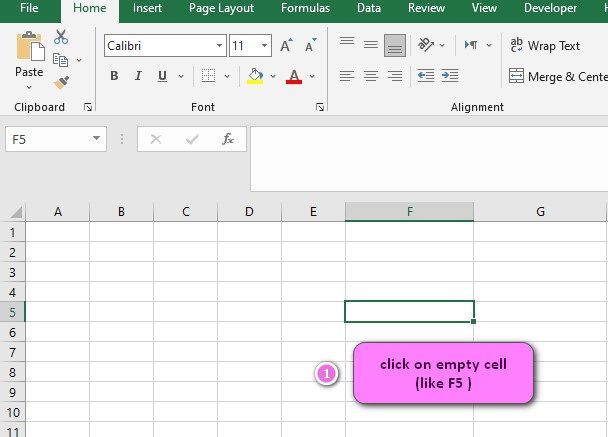
- Click on an empty cell (like F5 )
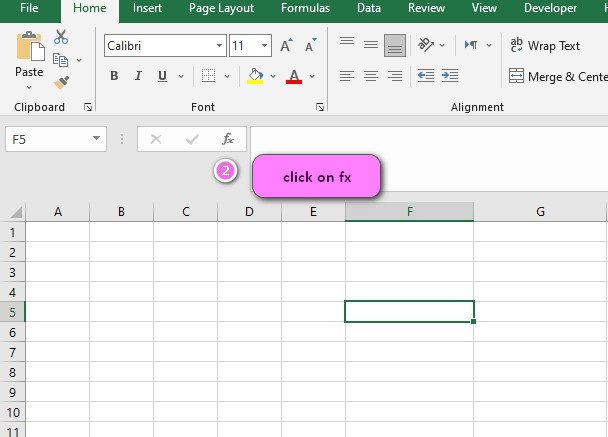
2. Click on the fx icon (or press shift+F3)
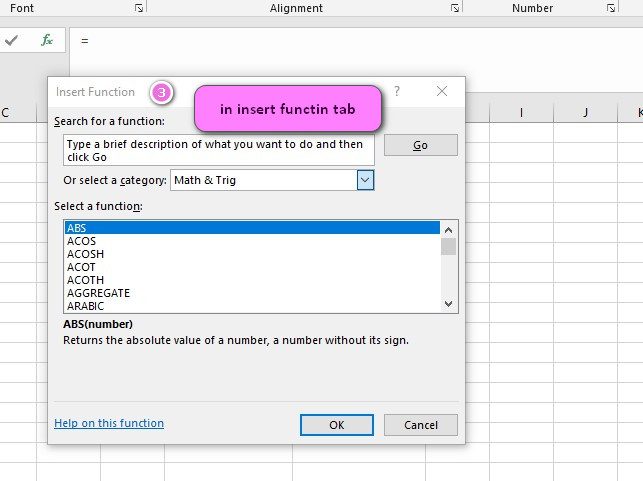
3. In the insert function tab you will see all functions
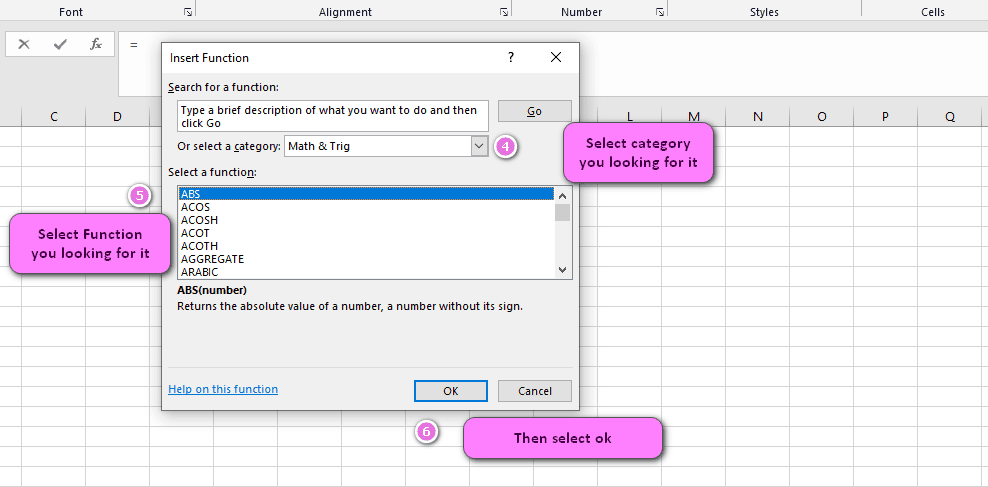
4. Select math and trig category
5. Select CSC function
6. Then select ok
7. In the function arguments Tab you will see CSC function
8. Number section is the angle in radians for which you want the cosecant
9. You will see results in the formula result section

Examples of CSC function in excel
- Finding the cosecant of an angle in radians:
=CSC(PI())
This would return the cosecant of pi radians (equal to 1).
- Finding the cosecant of an angle in degrees:
=CSC(RADIANS(45))
This would return the cosecant of 45 degrees (approximately 1.414).
- Using the CSC function in an array formula:
{=CSC(A1:A5)}
This would return an array of cosecant values for the angles in cells A1 through A5.
- Nesting the CSC function within other functions:
=SUM(CSC(A1),CSC(A2),CSC(A3))
This would find the sum of the cosecant values for the angles in cells A1, A2, and A3.
- Using the CSC function with the IF function:
=IF(CSC(A1)>1,"Greater than one","Less than or equal to one")
This would return “Greater than one” if the cosecant of the angle in cell A1 is greater than 1, and “Less than or equal to one” otherwise.
- Using the CSC function with conditional formatting:
Create a conditional formatting rule that highlights cells with cosecant values greater than some threshold value.
- Using the CSC function to find the length of the hypotenuse of a right triangle:
If you know an angle and the adjacent side of a right triangle, you can use the CSC function to find the length of the hypotenuse:
=1/COS(angle)*adjacent
Where angle is the angle in radians and adjacent is the length of the adjacent side.
- Using the CSC function to find the area of a triangle:
If you know two sides and an angle of a triangle, you can use the CSC function to find the height of the triangle and then use the formula for the area of a triangle:
=0.5*base*height
- Using the CSC function to find the intersection of two lines:
If you know the slopes and y-intercepts of two lines, you can use the CSC function to find the angle between them. Then, you can use trigonometry to find the point where they intersect.
- Using the CSC function to find the period of a sine or cosine function:
The period of a sine or cosine function is equal to 2*pi divided by the absolute value of the coefficient of x. You can use the CSC function to find the period of the function given its equation.
Example 1:
How to use CSC function in excel
You can see examples of CSC function below:

csc(A2) ----->>>>answer is 1
csc(A3) ----->>>>answer is 1.414
csc(A4) ----->>>>answer is -1
csc(A5) ----->>>>answer is 1.154
csc(A6) ----->>>>answer is 1CSC Function in Excel: What It Is and How to Use It
The CSC function is a trigonometric function in Excel that returns the cosecant of an angle. You can use the CSC function by entering “=CSC(angle)” into a cell, where “angle” is the angle (in radians) for which you want to find the cosecant. For example, if you want to find the cosecant of 0.5 radians, you would enter “=CSC(0.5)” into a cell.
Example: If we have an angle of 1.2 radians, we can use the CSC function in Excel by writing “=CSC(1.2)” in a cell to get the value of the cosecant of 1.2 radians.
Converting Degrees to Radians in Excel Made Easy
You can convert degrees to radians using the RADIANS function in Excel. For example, “=RADIANS(90)” would convert 90 degrees to pi/2 radians. To use this function, simply enter “=RADIANS(degrees)” into a cell, where “degrees” is the angle in degrees that you want to convert to radians.
Example: If we want to convert the angle 45 degrees to radians, we can use the RADIANS function in Excel by writing “=RADIANS(45)” in a cell to get the value of the angle in radians.
How to Convert Radians to Degrees Using Excel’s DEGREES Function
You can convert radians to degrees using the DEGREES function in Excel. For example, “=DEGREES(PI())” would convert pi radians to 180 degrees. To use this function, enter “=DEGREES(radians)” into a cell, where “radians” is the angle in radians that you want to convert to degrees.
Example: If we have an angle of 2.4 radians, we can convert it to degrees using the DEGREES function in Excel by writing “=DEGREES(2.4)” in a cell to get the value of the angle in degrees.
Understanding the Range of Values Returned by CSC Function in Excel
The CSC function in Excel returns real values between -infinity and -1 inclusive, or between 1 and infinity. For example, if you enter “=CSC(0)”, the result will be undefined because the cosecant of zero is infinity. If you enter “=CSC(1)”, the result will be approximately 1.1884 because the cosecant of one radian is approximately 1.1884.
Example: If we want to find the cosecant of an angle that is very close to 0 radians, say 0.00001 radians, the result will be approximately -100000 because the cosecant of 0.00001 radians is approximately -100000.
What Happens When You Try to Find Cosecant of an Angle with Sin(angle) = 0?
If you try to find the cosecant of an angle where the sine of that angle is equal to 0, you will receive a #DIV/0! error in Excel. This is because the definition of cosecant involves division by sine, which is not defined when sine equals 0.
Example: If we want to find the cosecant of an angle with sin(angle) = 0, say pi radians, the function “=CSC(SIN(PI()))” would result in a #DIV/0! error.
Why Can’t You Use Different Units of Measurement with the CSC Function in Excel?
The CSC function in Excel only accepts angles in radians as input. If you attempt to use other units of measurement, such as degrees or grads, you will receive an error.
Example: If we enter “=CSC(90)” in Excel, it will return a #VALUE! error because the function only accepts inputs in radians.
Using Array Formulas with CSC Function in Excel
You can use array formulas with the CSC function in Excel to perform calculations on multiple values simultaneously. To do this, simply enter the formula as normal, but instead of pressing “Enter”, press “Ctrl-Shift-Enter”. This will tell Excel to treat the formula as an array formula.
Example: If we want to find the cosecant of every angle in a range of cells A1:A5, we can use the array formula {=CSC(A1:A5)} to calculate the cosecant for all five angles at once.
Nesting CSC Function within Other Functions in Excel Explained
You can nest the CSC function within other functions in Excel to perform more complex calculations involving trigonometry. For example, you could use the CSC function as part of a formula to calculate the length of the hypotenuse of a right-angled triangle.
Example: If we want to find the length of the hypotenuse of a right-angled triangle with sides of length 3 and 4, we can use the formula “=SQRT(3^2+4^2)*CSC(ATAN(3/4))” in Excel. This formula uses the ATAN function to find the angle opposite the shorter side, then uses the CSC function to find the cosecant of that angle, and finally multiplies it by the length of the hypotenuse as found using the Pythagorean theorem.
Highlighting Cells Based on Their Cosecant Values using Conditional Formatting in Excel
You can use conditional formatting in Excel to highlight cells based on their cosecant values. To do this, select the cells you want to format, go to the “Conditional Formatting” menu, and create a new rule that uses the formula “=CSC(angle)>threshold”, where “angle” is the cell value containing the angle in radians, and “threshold” is the minimum value for which you want the cell to be highlighted.
Example: If we want to highlight any cell whose cosecant value is greater than 5, we can select the range of cells, create a new conditional formatting rule, and enter the formula “=CSC(A1)>5”.
Using CSC Function to Find Length of Hypotenuse of a Right Triangle in Excel
You can use the CSC function in Excel to find the length of the hypotenuse of a right triangle if you know the lengths of the other two sides. The formula is simply “hypotenuse = side / CSC(angle)”, where “side” is the length of one of the other sides, and “angle” is the angle opposite that side in radians.
Example: If we have a right triangle with sides of length 3 and 4, we can use the formula “=3/CSC(ATAN(3/4))” in Excel to find the length of the hypotenuse.
Calculating Triangle Area with CSC Function in Excel
You can use the CSC function in Excel to calculate the area of a triangle if you know the lengths of two sides and the included angle. The formula is simply “area = 0.5 * side1 * side2 * CSC(angle)”, where “side1” and “side2” are the lengths of the two sides, and “angle” is the included angle in radians.
Example: If we have a triangle with sides of length 3 and 4, and the included angle is pi/3 radians, we can use the formula “=0.534*CSC(PI()/3)” in Excel to find the area of the triangle.
Finding Intersection of Two Lines with CSC Function in Excel
You can use the CSC function in Excel to find the intersection point of two lines in a Cartesian coordinate system. The formula is simply “x = (y – y1) / CSC(angle) + x1”, where “angle” is the angle of one of the lines in radians, and “x1” and “y1” are the coordinates of any point on that line.
Example: If we have two lines, one with an angle of pi/4 radians and passing through the point (2,0), and one with an angle of 3pi/4 radians and passing through the point (0,3), we can use the formula “=((3-0)/CSC(3PI()/4))+0″ in Excel to find the x-coordinate of the intersection point. This gives us x=3.
Understanding the Period of Sine or Cosine Function in Excel
The period of a sine or cosine function in Excel is the distance between two corresponding points on the graph. For standard sine and cosine functions, the period is 2π radians for both.
Example: If we have the function “=SIN(x)” in Excel, the period will be 2π radians, meaning that the value of the function will repeat every 2π radians.
How to Find Accuracy of Results with CSC Function in Excel
You can find the accuracy of results obtained using the CSC function in Excel by comparing them to known values or values obtained using other methods. One way to do this is to use the TAN function to find the tangent of the angle, and then divide 1 by the result to obtain the cosecant.
Example: If we want to find the cosecant of an angle of 1.5 radians, we can use the formula “=1/TAN(1.5)” in Excel to obtain an approximate result of 3.638. We can then compare this to the actual cosecant value obtained through other means to determine the accuracy of the result.
What Happens When You Try to Find Cosecant of an Angle with Cos(angle) = 0?
If you try to find the cosecant of an angle where the cosine of that angle is equal to 0, you will receive a #DIV/0! error in Excel. This is because the definition of cosecant involves division by cosine, which is not defined when cosine equals 0.
Example: If we want to find the cosecant of an angle with cos(angle) = 0, say π/2 radians, the function “=CSC(COS(PI()/2))” would result in a #DIV/0! error.
Limitations of the CSC Function in Excel with Complex Numbers
The CSC function in Excel is not defined for complex numbers. If you try to use it with a complex number, you will receive a #NUM! error.
Example: If we want to find the cosecant of a complex number, say 2+3i, the function “=CSC(2+3i)” would result in a #NUM! error.
How to Find Inverse Cosecant of a Number in Excel
You can find the inverse cosecant of a number in Excel using the ACSC function. The formula for finding the inverse cosecant of a number x is “=ACSC(x)”, where x is the value for which you want to find the inverse cosecant.
Example: If we want to find the inverse cosecant of 2, we can use the formula “=ACSC(2)” in Excel to obtain the angle whose cosecant is 2. Note that this function returns the result in radians.

