What is GAMMA.DIST function in Excel?
The GAMMA.DIST function is one of the Statistical functions of Excel.
It returns the gamma distribution.
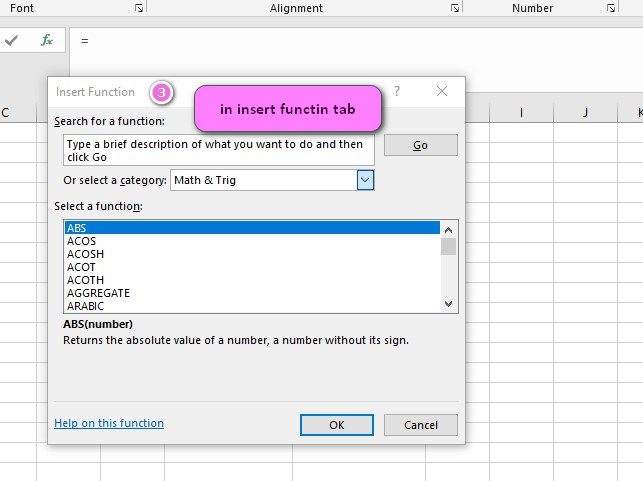
We can find this function in Statistical of insert function Tab.
How to use GAMMA.DIST function in excel
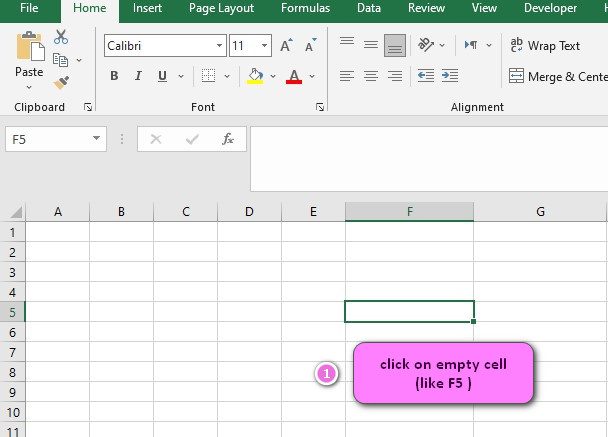
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).

3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select GAMMA.DIST function.
6. Then select ok.

7. In the function arguments Tab you will see GAMMA.DIST function.
8. X is the value at which you want to evaluate the distribution, a non-negative number.
9. Alpha is a parameter to the distribution, a positive number.
10. Beta is a parameter to the distribution, a positive number. If beta = 1, GAMMA.DIST returns the standard gamma distribution.
11. Cumulative is a logical value: return the cumulative distribution function = TRUE; return the probability mass function = FALSE or omitted.
12. You will see the results in the formula result section.
Examples of GAMMA.DIST function in Excel
here are 10 examples of the gamma.dist function in Excel:
- To find the probability density of the gamma distribution with a shape parameter of 3 and a scale parameter of 2 at a value of 5, use the formula: =GAMMA.DIST(5,3,2,TRUE)
- To find the cumulative distribution of the gamma distribution with a shape parameter of 4 and a scale parameter of 6 at a value of 8, use the formula: =GAMMA.DIST(8,4,6,TRUE)
- To find the probability density of the gamma distribution with a shape parameter of 1.5 and a scale parameter of 0.5 at a value of 2, use the formula: =GAMMA.DIST(2,1.5,0.5,TRUE)
- To find the cumulative distribution of the gamma distribution with a shape parameter of 7 and a scale parameter of 3 at a value of 15, use the formula: =GAMMA.DIST(15,7,3,TRUE)
- To find the probability density of the gamma distribution with a shape parameter of 2.3 and a scale parameter of 4.5 at a value of 3, use the formula: =GAMMA.DIST(3,2.3,4.5,TRUE)
- To find the cumulative distribution of the gamma distribution with a shape parameter of 5 and a scale parameter of 2 at a value of 10, use the formula: =GAMMA.DIST(10,5,2,TRUE)
- To find the probability density of the gamma distribution with a shape parameter of 1.8 and a scale parameter of 1 at a value of 2.5, use the formula: =GAMMA.DIST(2.5,1.8,1,TRUE)
- To find the cumulative distribution of the gamma distribution with a shape parameter of 6 and a scale parameter of 4 at a value of 12, use the formula: =GAMMA.DIST(12,6,4,TRUE)
- To find the probability density of the gamma distribution with a shape parameter of 2.5 and a scale parameter of 3.5 at a value of 4, use the formula: =GAMMA.DIST(4,2.5,3.5,TRUE)
- To find the cumulative distribution of the gamma distribution with a shape parameter of 3.2 and a scale parameter of 5 at a value of 8, use the formula: =GAMMA.DIST(8,3.2,5,TRUE)
What is the GAMMA.DIST function used for?
The GAMMA.DIST function in Excel is used to calculate the probability density or cumulative distribution of a random variable that follows a gamma distribution.
It can be used to model various phenomena such as the time between failures, insurance claims and rainfall.
How do I use the GAMMA.DIST function in Excel?
The syntax for the GAMMA.DIST function is as follows: GAMMA.DIST(x, alpha, beta, cumulative) where x is the value at which you want to evaluate the function.
alpha and beta are the shape and scale parameters of the gamma distribution respectively, and cumulative is a logical value that determines whether to calculate the probability density (FALSE) or cumulative distribution (TRUE).
For example, to calculate the probability density of a gamma distribution with shape parameter alpha = 2 and scale parameter beta = 3 at x = 4, you would use the following formula: GAMMA.DIST(4, 2, 3, FALSE) which returns 0.0654.
What are the arguments of the GAMMA.DIST function?
The GAMMA.DIST function takes four arguments:
- x: The value at which you want to evaluate the function.
- alpha: The shape parameter of the gamma distribution.
- beta: The scale parameter of the gamma distribution.
- cumulative: A logical value that determines whether to calculate the probability density (FALSE) or cumulative distribution (TRUE).
What is the syntax of the GAMMA.DIST function?
The syntax for the GAMMA.DIST function is as follows: GAMMA.DIST(x, alpha, beta, cumulative)
Can the GAMMA.DIST function be used for probability density or cumulative distribution? Yes, the GAMMA.DIST function can be used to calculate both the probability density and cumulative distribution of a gamma distribution, depending on the value of the cumulative argument.
If cumulative is set to FALSE (or omitted), the function returns the probability density at x. If cumulative is set to TRUE, the function returns the cumulative distribution up to x.
How does the GAMMA.DIST function work?
The GAMMA.DIST function in Excel calculates the probability density or cumulative distribution of a gamma distribution at a given value x, using the shape and scale parameters alpha and beta.
The formula used to calculate the probability density is: (x^(alpha-1) * e^(-x/beta)) / (beta^alpha * Gamma(alpha)) where Gamma is the gamma function.
The formula used to calculate the cumulative distribution is: GAMMA.DIST(x, alpha, beta, TRUE) which is equivalent to: I(alpha, x/beta)
Where I is the regularized incomplete gamma function.
What is the difference between GAMMA.DIST and GAMMA.INV functions?
The GAMMA.DIST function calculates the probability density or cumulative distribution of a gamma distribution at a given value x, while the GAMMA.INV function calculates the inverse of the cumulative distribution at a given probability level.
In other words, GAMMA.DIST returns the probability of observing a value less than or equal to x, while GAMMA.INV returns the value that corresponds to a given probability level.
What is the domain of the GAMMA.DIST function?
The domain of the GAMMA.DIST function is all real numbers greater than or equal to zero for the argument x, and positive real numbers for the arguments alpha and beta.
Can negative values be used as arguments in the GAMMA.DIST function?
No, negative values cannot be used as arguments in the GAMMA.DIST function because the gamma distribution is only defined for non-negative values.
How accurate is the GAMMA.DIST function?
The accuracy of the GAMMA.DIST function depends on the values of the arguments and the computational precision of the computer.
The function is generally accurate for most practical purposes, but errors can occur when evaluating very small probabilities or very large values of x.
It is recommended to compare the results of the GAMMA.DIST function with those obtained using other statistical software or reference tables to ensure accuracy.
What are some common errors when using the GAMMA.DIST function?
Common errors when using the GAMMA.DIST function include providing negative values for the arguments x, alpha, or beta, or omitting any of the required arguments.
Another common error is providing an invalid value for the cumulative argument, since it must be either TRUE or FALSE.
What is the gamma distribution?
The gamma distribution is a continuous probability distribution that is often used to model the time between events occurring at a constant rate, such as the time between phone calls in a call center or the time between arrivals of customers at a store.
The gamma distribution has two parameters: shape (α) and scale (β).
When should I use the gamma distribution?
The gamma distribution is commonly used when modeling the waiting times between independent events that occur at a constant rate over time.
It can also be used to model various phenomena such as radioactive decay, insurance claims, and rainfall. In general, the gamma distribution is suitable for situations where the data has a skewed, positive tail.
What are the properties of the gamma distribution? Some of the key properties of the gamma distribution include:
- The mean of the gamma distribution is αβ.
- The variance of the gamma distribution is αβ^2.
- The shape parameter α determines the skewness of the distribution, with larger values of α resulting in less skewness.
- The scale parameter β determines the overall spread of the distribution.
How can I generate a random sample from the gamma distribution in Excel?
You can generate a random sample from the gamma distribution in Excel using the GAMMA.INV function.
The formula for generating a random sample with shape parameter α and scale parameter β is: GAMMA.INV(RAND(), α, β) where RAND() generates a random number between 0 and 1.
Repeat this formula as many times as needed to generate the desired sample size.
How can I plot the gamma distribution in Excel?
To plot the gamma distribution in Excel, you can use the GAMMA.DIST function combined with a charting tool like Excel’s built-in graphing capabilities or a third-party add-on like Excel’s Data Analysis Toolpak. Here are the steps:
- Enter the shape and scale parameters of the gamma distribution into separate cells in your worksheet.
- Use the GAMMA.DIST function in another cell to calculate the probability density at various points along the x-axis of your chart.
- Select the range of x-axis values and the corresponding probabilities to be plotted.
- Insert a chart from the “Insert” tab and select the appropriate chart type for your data.
What are some examples of using the GAMMA.DIST function in real-life scenarios?
The GAMMA.DIST function can be used in a variety of real-life scenarios where we want to model the behavior of a random variable that follows a gamma distribution. For example:
- In finance, the gamma distribution is used to model stock prices and interest rates. The GAMMA.DIST function can be used to calculate the probability of different price or rate movements over a certain time period.
- In healthcare, the gamma distribution is used to model the distribution of patient lengths of stay or time until recovery. The GAMMA.DIST function can be used to calculate the probability of different lengths of stay or times until recovery.
- In manufacturing, the gamma distribution is used to model the time it takes to complete a production process. The GAMMA.DIST function can be used to calculate the probability of completing the process within a certain timeframe.
Can the GAMMA.DIST function be used in financial analysis?
Yes, the GAMMA.DIST function can be used in financial analysis to model the behavior of stock prices, interest rates, and other financial variables that follow a gamma distribution.
For example, it can be used to calculate the probability of a stock price moving up or down by a certain amount over a given time period.
How does changing the shape and scale parameters affect the shape of the gamma distribution?
The shape and scale parameters of the gamma distribution determine the shape, location, and spread of the distribution.
Generally, increasing the shape parameter makes the distribution more skewed and longer-tailed, while increasing the scale parameter shifts the distribution to the right and increases its variance.
For example, consider two gamma distributions with the same shape parameter but different scale parameters.
The distribution with the larger scale parameter will have a higher mean and variance and be shifted further to the right on the x-axis. Conversely, two gamma distributions with the same scale parameter but different shape parameters will have different levels of skewness and kurtosis.
Are there any limitations to using the GAMMA.DIST function?
One limitation of using the GAMMA.DIST function is that it assumes that the input parameters are valid and that the data follows a gamma distribution.
If the data does not follow a gamma distribution, the results may be inaccurate or misleading.
Additionally, when fitting a gamma distribution to data, it is important to ensure that the data is sufficiently large and representative of the population being modeled.
Otherwise, the resulting model may not accurately reflect the underlying distribution of the data.