What is HARMEAN function in Excel?
The HARMEAN function is one of the Statistical functions of Excel.
It returns the harmonic mean of a data set of positive numbers: the reciprocal of the arithmetic mean of reciprocals.
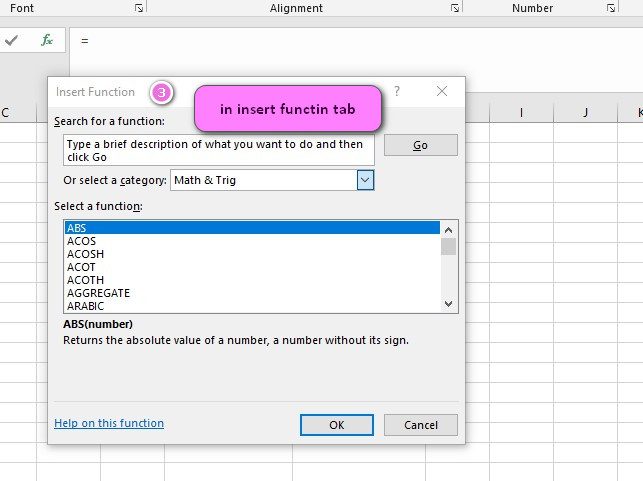
We can find this function in Statistical category of insert function Tab.
How to use HARMEAN function in excel
- Click on an empty cell (like F5).
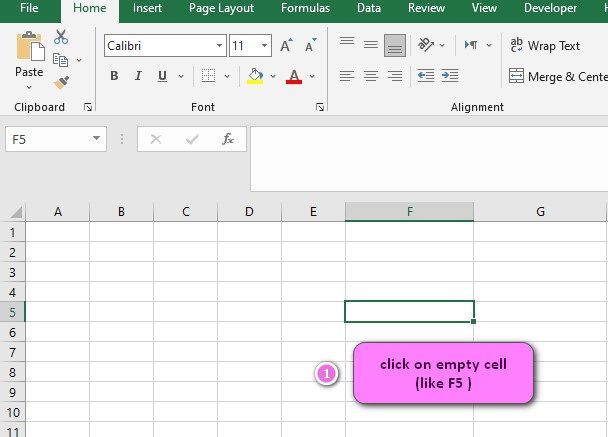
2. Click on the fx icon (or press shift+F3).
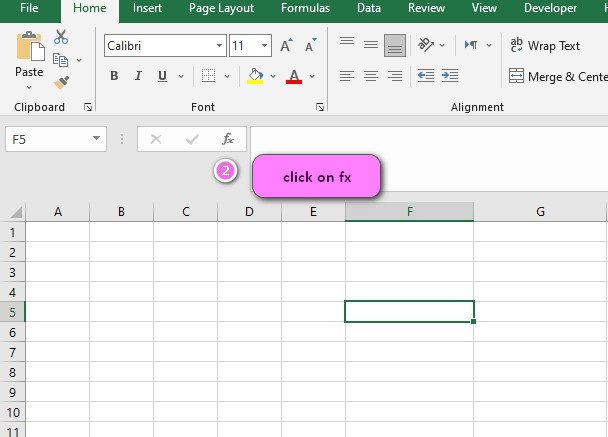
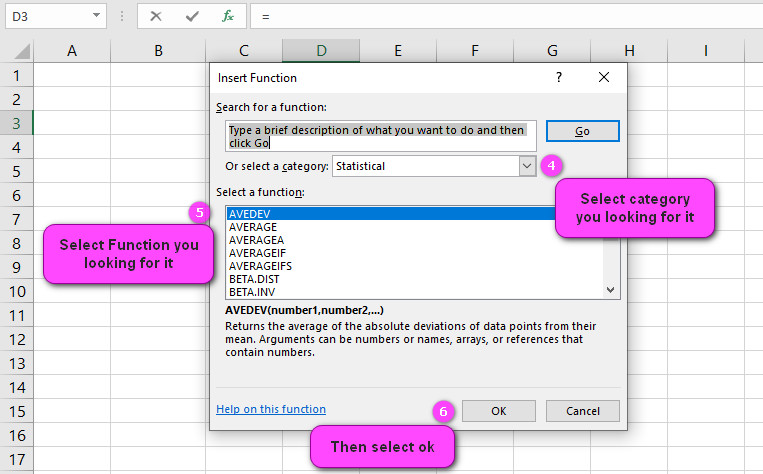
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select HARMEAN function.
6. Then select ok.
7. In the function arguments Tab you will see HARMEAN function.
8. Number1: number1,number2,… are 1 to 255 numbers or names, arrays, or references that contain numbers for which you want the harmonic mean.
9. Number2: number1,number2,… are 1 to 255 numbers or names, arrays, or references that contain numbers for which you want the harmonic mean.
10. You will see the results in the formula result section.
Examples of HARMEAN function in Excel
The HARMEAN function in Excel is used to calculate the harmonic mean of a set of numbers.
Here are 10 examples of using the HARMEAN function:
- To calculate the harmonic mean of the numbers in cells A1 through A5:=HARMEAN(A1:A5)
- To calculate the harmonic mean of the numbers 2, 4, and 8:=HARMEAN(2, 4, 8)
- To calculate the harmonic mean of the numbers in a named range called “Sales”:=HARMEAN(Sales)
- To calculate the harmonic mean of the numbers in a table column called “Expenses”:=HARMEAN(Table1[Expenses])
- To calculate the harmonic mean of the numbers in a filtered table column called “Revenue”:=HARMEAN(SUBTOTAL(9,Table1[Revenue]))
- To calculate the harmonic mean of the numbers in a range that includes blank cells:=HARMEAN(A1,A2,,A4,A5)
- To calculate the harmonic mean of the absolute values of the numbers in a range:=HARMEAN(ABS(A1:A5))
- To calculate the harmonic mean of the reciprocals of the numbers in a range:=HARMEAN(1/A1:A5)
- To calculate the harmonic mean of the square roots of the numbers in a range:=HARMEAN(SQRT(A1:A5))
- To calculate the harmonic mean of the logarithms of the numbers in a range:=HARMEAN(LOG(A1:A5))
When would it be appropriate to use the HarMean and GeoMean formulas?
The choice of using Harmonic Mean (HarMean) or Geometric Mean (GeoMean) formulas depends on the nature of the data and what you want to measure.
Harmonic Mean is generally used when dealing with rates, ratios, or frequencies. It is appropriate when you want to calculate the average rate at which a value is changing over time or when you want to find an average of ratios or proportions.
For example, if you want to find the average speed of a car during a trip, you could use HarMean, as it takes into account the time spent driving at different speeds.
On the other hand, Geometric Mean is generally used when dealing with growth rates or comparing values that have different magnitudes.
It is appropriate when you want to find an average rate of change or an average factor of increase or decrease.
For example, if you want to find the average annual growth rate of a company’s revenue over multiple years, you could use GeoMean.
In terms of using these formulas with non-response data points, it may be preferable to exclude those non-response data points from your analysis or replace them with an appropriate value such as the mean or median of the responding data points, depending on the context and nature of the data.
Examples of HARMEAN function in Excel
What is the HARMEAN function in Excel?
The HARMEAN function in Excel is a mathematical function that calculates the harmonic mean of a set of numbers.
The harmonic mean is a type of average used to calculate the average rate or speed, and it is calculated by dividing the number of values in the set by the sum of their reciprocals.
For example, suppose you have the following five values: 10, 20, 30, 40, and 50.
To calculate the harmonic mean of these numbers using the HARMEAN function, you would use the following formula:
=HARMEAN(10, 20, 30, 40, 50)
This would return a value of 22.22222.
Another example of using the HARMEAN function in Excel could involve calculating the average speed of a vehicle over a given distance.
Suppose a car traveled 100 km at 60 km/h, then 200 km at 80 km/h, and finally 100 km at 70 km/h. The average speed of the car can be calculated using the harmonic mean, as follows:
=HARMEAN(3, 100/60, 200/80, 100/70)
This formula takes into account both the distances traveled and the speeds at which they were traveled, resulting in a more accurate average speed of approximately 67.9 km/h.
In summary, the HARMEAN function in Excel is a useful tool for calculating the harmonic mean of a set of values, which can be particularly relevant in situations where rates or speeds need to be averaged.
How does the HARMEAN function differ from other averaging functions in Excel?
The HARMEAN function in Excel calculates the harmonic mean of a set of numbers. This type of average is useful when working with rates or ratios.
Unlike the more commonly used arithmetic mean, which is calculated by adding up all the values in a dataset and dividing by the number of values, the harmonic mean is calculated by taking the reciprocal of each value, finding their average, and then taking the reciprocal of that average.
Here’s an example to illustrate the difference between the two: Let’s say you’re calculating the average speed of a car over a certain distance.
The car travels at 60 mph for half the distance and 40 mph for the other half. The arithmetic mean would be (60 + 40) / 2 = 50 mph.
However, this value doesn’t take into account the fact that the car spent equal amounts of time traveling at both speeds.
To calculate the harmonic mean, we first take the reciprocals of the speeds: 1/60 and 1/40. Then we find the average of these values: (1/60 + 1/40)/2 = 1/48. Finally, we take the reciprocal of this average to get the harmonic mean: 48 mph.
Other averaging functions in Excel include:
- AVERAGE: Calculates the arithmetic mean of a set of numbers.
- MEDIAN: Finds the middle value in a set of numbers.
- MODE: Returns the most frequently occurring value in a set of numbers.
- GEOMEAN: Calculates the geometric mean of a set of positive numbers.
Each of these functions has its own specific use cases and should be chosen based on the type of data being analyzed.
What are the required arguments for the HYPGEOM.DIST function?
The HYPGEOM.DIST function is a statistical function in Microsoft Excel that calculates the probability of a certain number of successes in a specified population, given a sample size and number of successes.
This function is commonly used in hypothesis testing and statistical analysis.
The required arguments for the HYPGEOM.DIST function are:
x– The number of successes in the sample.N– The population size.M– The number of successes in the population.n– The sample size.
These arguments are used to calculate the probability of obtaining x successes in a sample of size n, when there are M total successes in a population of size N.
Here’s an example of how to use the HYPGEOM.DIST function in Excel:
Suppose you have a population of 500 people, of which 250 are women. You randomly select a sample of 50 people from the population. You want to know the probability of getting exactly 20 women in your sample.
To calculate this probability using the HYPGEOM.DIST function, you would use the following formula:
=HYPGEOM.DIST(20,500,250,50,FALSE)
In this formula:
20represents the number of women you want to get in your sample.500represents the total population size.250represents the total number of women in the population.50represents the sample size.FALSEspecifies that you want to get the probability of exactlyxsuccesses, rather than the probability ofxor fewer successes.
This formula will return the probability of getting exactly 20 women in your sample, given the population and sample sizes.
Can the HARMEAN function be used for non-numeric values in Excel?
This function is specifically meant for numeric values and cannot be used for non-numeric values.
The harmonic mean is calculated by dividing the total number of values in the set by the sum of the reciprocals of those values.
Since the reciprocal of a non-numeric value cannot be calculated, it is not possible to use the HARMEAN function for non-numeric values.
Here is an example of using the HARMEAN function in Excel with a set of numeric values:
Suppose we have a list of numbers: 2, 4, 8, and 16. We can use the HARMEAN function in Excel to find their harmonic mean by entering the formula “=HARMEAN(2,4,8,16)” into a cell.
The result will be 4. In this case, the harmonic mean tells us that the “typical” value in the set is closer to 4 than to any other value.
However, if we try to use the HARMEAN function with non-numeric values, such as “apple”, “banana”, and “orange”, Excel will return an error message because these values cannot be converted to numeric values for the calculation of the harmonic mean.
How accurate is the HARMEAN function in Excel?
The harmonic mean is a type of average that is used to calculate the average rate of change over time, such as the average speed of a car on a journey.
The accuracy of the HARMEAN function in Excel depends on how well it is used and whether it is being applied to an appropriate set of data.
When used correctly, it can provide an accurate measure of the harmonic mean of a set of numbers.
For example, let’s say we want to calculate the harmonic mean of the numbers 2, 4, and 8. We can use the following formula in Excel:
=HARMEAN(2,4,8)
The result will be 3.2, which is the harmonic mean of the three numbers.
However, if we were to apply the same function to a set of numbers that is not appropriate for calculating a harmonic mean, the result may not be accurate.
For instance, calculating the harmonic mean of test scores or weights of different items would not be appropriate.
In summary, the HARMEAN function in Excel can be accurate when used correctly and with appropriate data.
It is important to ensure that the data being analyzed is suitable for calculating the harmonic mean before using this function.
Can the HARMEAN function handle arrays or ranges of values in Excel?
he HARMEAN function is used to calculate the harmonic mean of a set of numbers in Excel.
Harmonic mean is a type of average that is calculated by dividing the number of values in a set by the reciprocal of each value, and then taking the reciprocal of the resulting sum.
Here’s an example of how to use the HARMEAN function with an array of values:
Suppose you have an array of values in cells A1 through A5, and you want to find the harmonic mean of these values. You can use the following formula:
=HARMEAN(A1:A5)
This will return the harmonic mean of the values in cells A1 through A5.
You can also use the HARMEAN function with a range of values.
For example, suppose you have a range of values in cells B1 through B10, and you want to find the harmonic mean of the first five values. You can use the following formula:
=HARMEAN(B1:B5)
This will return the harmonic mean of the values in cells B1 through B5.
In conclusion, the HARMEAN function can be used with arrays or ranges of values in Excel, making it a useful tool for calculating the harmonic mean of large datasets.
Are there any limitations when using the HARMEAN function in Excel?
The HARMEAN function in Excel is used to find the harmonic mean of a set of numbers.
It is a mathematical formula that calculates the reciprocal of the arithmetic mean of the reciprocals of the given numbers.
While the HARMEAN function can be useful in certain situations, there are some limitations to its use:
- Limited applicability: The harmonic mean is most useful when dealing with rates or ratios, such as speed or efficiency. It may not be as relevant for other types of data.
- Sensitivity to extreme values: The harmonic mean is highly sensitive to extreme values, such as outliers. This means that even a single outlier can have a significant impact on the calculated value, and may not provide an accurate reflection of the dataset as a whole.
- Need for non-zero values: Another limitation of the HARMEAN function is that it requires all values to be non-zero. If any of the values are zero, the function will return an error.
Here’s an example to illustrate the use of the HARMEAN function:
Suppose you have a dataset representing the time taken by five runners to complete a race:
Runner 1: 10 seconds Runner 2: 15 seconds Runner 3: 20 seconds Runner 4: 25 seconds Runner 5: 30 seconds
To calculate the harmonic mean of these values using the HARMEAN function in Excel, you could enter the following formula into a cell:
=HARMEAN(10,15,20,25,30)
This would give you a result of 17.14 seconds, which represents the average rate at which the runners completed the race.
However, as mentioned earlier, this value may not provide an accurate representation of the dataset if there are outliers or zero values present.
How can I use the HARMEAN function effectively in my Excel worksheets?
To use the HARMEAN function in Excel, follow these steps:
- Select the cell where you want the result to appear.
- Type “=HARMEAN(” into the formula bar.
- Select the range of cells containing the values for which you want to calculate the harmonic mean. You can also manually enter each value separated by commas.
- Close the parentheses and press Enter.
Here’s an example of how to use the HARMEAN function in Excel:
Suppose you are tracking the speeds of several cars during a race, and you want to calculate the overall average speed of the race.
You have recorded the speeds of each car after each lap, and you want to calculate the harmonic mean of these speeds to account for any changes in speed throughout the race.
In this scenario, you could use the HARMEAN function in Excel to calculate the harmonic mean of the speeds.
To do this, you would select the range of cells containing the speeds, and enter the function “=HARMEAN(A2:A10)” (assuming the speeds are stored in cells A2 through A10).
This would give you the harmonic mean of the speeds for the entire race.
I hope this explanation helps you understand how to use the HARMEAN function in Excel more effectively! If you have any further questions or need additional assistance, feel free to ask.
Can the HARMEAN function be combined with other Excel functions to perform more complex calculations?
Here are a few examples of how you could combine the HARMEAN function with other Excel functions:
- Using the
HARMEANfunction with theSUMfunction: You could use theSUMfunction to find the sum of a set of numbers, and then divide that sum by the number of values in the set. Finally, you can use theHARMEANfunction to calculate the harmonic mean of those numbers. For example, if you have the numbers 2, 4, and 8 in cells A1, A2, and A3 respectively, you could use the formula=HARMEAN(A1:A3)to find their harmonic mean. - Using the
HARMEANfunction with theAVERAGEfunction: You could use theAVERAGEfunction to find the arithmetic mean of a set of numbers, and then use theHARMEANfunction to find the harmonic mean of their reciprocals. For example, if you have the numbers 2, 4, and 8 in cells A1, A2, and A3 respectively, you could use the formula=HARMEAN(1/A1:1/A3)to find their harmonic mean. - Using the
HARMEANfunction with theCOUNTIFfunction: You could use theCOUNTIFfunction to count the number of values in a set that meet a certain criteria, and then use theHARMEANfunction to find the harmonic mean of those values. For example, if you have the numbers 2, 4, 6, and 8 in cells A1, A2, A3, and A4 respectively, and you want to find the harmonic mean of the values that are greater than or equal to 4, you could use the formula=HARMEAN(IF(A1:A4>=4,1/A1:A4)).