What is LINEST function in Excel?
The LINEST function is one of the Statistical functions of Excel.
It Returns statistics that describe a linear trend matching known data points, by fitting a straight line using the least squares method.
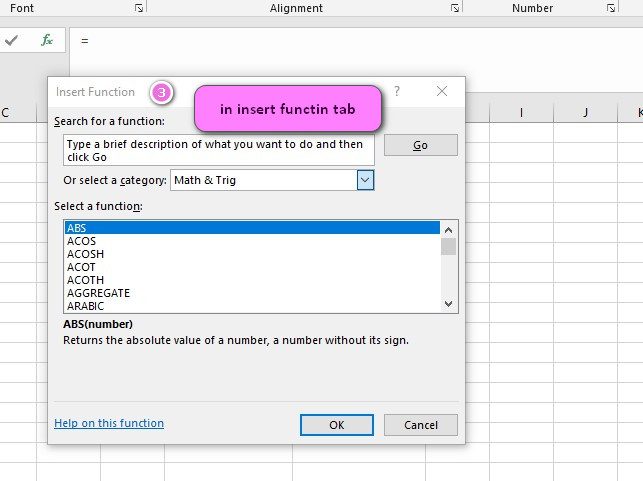
We can find this function in Statistical category of the insert function Tab.
How to use LINEST function in excel
- Click on an empty cell (like F5).
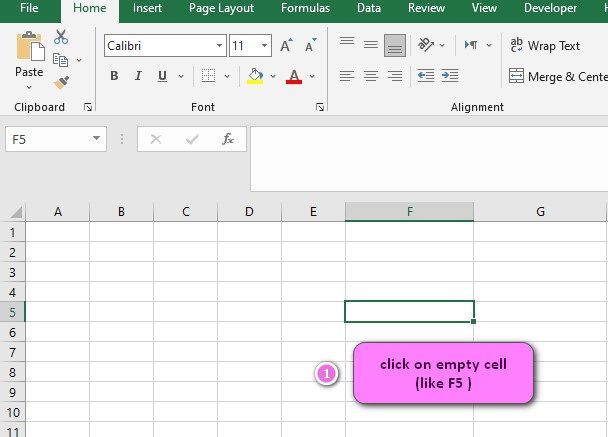
2. Click on the fx icon (or press shift+F3).
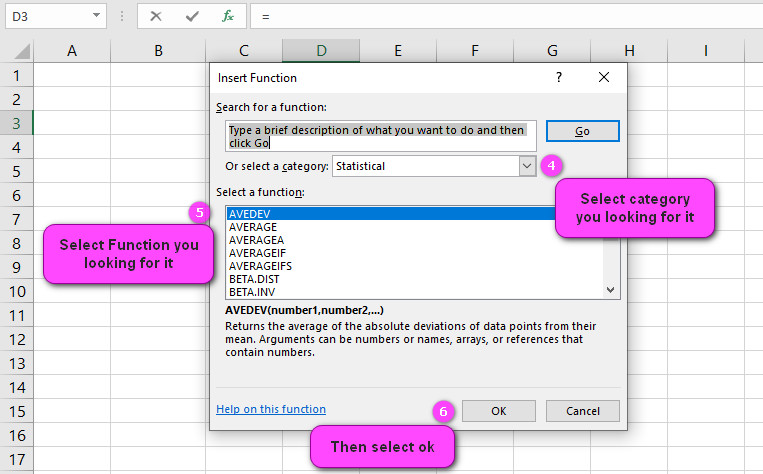
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select LINEST function.
6. Then select ok.
7. In the function arguments Tab you will see LINEST function.
8. Known_ys is the set of y-values you already know in the relationship y = mx + b.
9. Known_xs is an optional set of x-values that you may already know in the relationship y = mx + b.
10. Const is a logical value: the constant b is calculated normally if Const = TRUE or omitted; b is set equal to 0 if Const = FALSE.
11. Stats is a logical value: return additional regression statistics = TRUE; return m-coefficients and the constant b = FALSE or omitted.
12. You will see the results in the formula result section.
What is the syntax of LINEST function?
The LINEST function is used to calculate the statistics for a line that best fits a set of data points. The function returns an array of values that can be used to generate the regression line equation.
Here’s the syntax for the LINEST function:
=LINEST(known_y’s, [known_x’s], [const], [stats])
- known_y’s: This is a required input and represents the array or range of dependent variables (y-values) that are being studied.
- known_x’s: This is an optional input and represents the array or range of independent variables (x-values) that correspond to the dependent variables. If this parameter is omitted, Excel assumes a set of sequential integers starting from 1.
- const: This is an optional input that specifies whether to force the intercept to be zero. If omitted, the function will calculate an intercept.
- stats: This is an optional input that specifies which additional statistics should be returned alongside the coefficients. If omitted, the function will only return the coefficients.
Let’s take a look at an example of how to use the LINEST function in Excel:
Suppose we have the following set of data points:
| X | Y |
|---|---|
| 1 | 3 |
| 2 | 5 |
| 3 | 7 |
| 4 | 9 |
| 5 | 11 |
To find the line of best fit for these data points, we can use the LINEST function in Excel as follows:
- Select a blank cell where you want to display the results.
- Enter the formula “=LINEST(B2:B6, A2:A6)” (without quotes). This tells Excel to calculate the LINEST function for the y-values in column B and the corresponding x-values in column A.
- Press Enter to calculate the function.
Excel will return an array of values that can be used to generate the regression line equation. The output might look something like this:
| A | B | |
|---|---|---|
| 1 | ||
| 2 | 1 | 3 |
| 3 | 2 | 5 |
| 4 | 3 | 7 |
| 5 | 4 | 9 |
| 6 | 5 | 11 |
| 7 | ||
| 8 | ||
| 9 | Coefficients: | |
| 10 | Intercept: | 1 |
| 11 | Slope: | 2 |
| 12 |
In this example, we see that the LINEST function has returned a slope of 2 and an intercept of 1. We can use these values to generate the regression line equation as follows:
y = 2x + 1
So, if we wanted to predict the value of y for an x-value of 6, we could plug that value into the equation:
y = 2(6) + 1 = 13
Therefore, the predicted value of y for an x-value of 6 would be 13.
What does LINEST function do in Excel?
Let’s look at an example to better understand how to use the LINEST function in Excel. Suppose we have the following set of data:
| X | Y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
To find the slope and y-intercept for the line of best fit, we can use the LINEST function as follows:
- Select a range of cells where you want to display the LINEST results.
- Enter the following formula: =LINEST(B2:B5,A2:A5)
- Press Ctrl + Shift + Enter to enter the formula as an array formula.
This will return an array of information that includes the slope and y-intercept values for the line of best fit:
| A | B | |
|---|---|---|
| Slope | 2 | |
| Intercept | 0 |
We can see that the slope of the line is 2 and the y-intercept is 0. This means that the equation for the line of best fit is y = 2x.
In addition to the slope and y-intercept, we can also use the LINEST function to calculate other regression statistics such as the correlation coefficient and standard error.
To do this, we need to add two more arguments to the formula:
=LINEST(B2:B5,A2:A5,TRUE,TRUE)
This will return an array that includes the following additional statistics:
| A | B | |
|---|---|---|
| Slope | 2 | |
| Intercept | 0 | |
| R-squared | 1 | |
| Std. Error | 0 |
The R-squared(r2) value indicates how well the line of best fit fits the data, with a value of 1 indicating a perfect fit.
The standard error represents the average distance between the actual data points and the predicted values on the line of best fit.
Overall, the LINEST function is a powerful tool in Excel that can help you quickly calculate important regression statistics for a set of data.
How do enter LINEST function into an Excel worksheet?
The LINEST function is used to calculate the statistics for a line by using the least squares method to calculate the line’s slope and y-intercept. Here are the steps to enter the LINEST function into an Excel worksheet:
Step 1: Select the cell where you want to display the result of the LINEST function.
Step 2: Type =LINEST( to start the function.
Step 3: Highlight the range of the dependent variable data. This is the y-values of the data that you want to fit with a line.
Step 4: Type a comma (,) to separate the arguments.
Step 5: Highlight the range of the independent variable data. This is the x-values of the data that you want to fit with a line.
Step 6: Type another comma (,) to separate the arguments.
Step 7: Type TRUE or 1 to indicate that you want the LINEST function to return additional regression statistics, such as r-squared and standard error. Alternatively, type FALSE or 0 if you only want the slope and intercept.
Step 8: Close the function with a closing parenthesis ()) and press Enter.
Here is an example of how to use the LINEST function in Excel: Suppose we have the following data in two columns, representing x and y values:
X Y
1 2
2 4
3 6
4 8
5 10
To find the slope and y-intercept of the line that best fits this data, we would use the LINEST function as follows:
- Select the cell where you want to display the LINEST results, say cell A8.
- Type “=LINEST(B2:B6,A2:A6,TRUE)” without quotes into cell A8.
- Press Enter.
The result will be displayed in cell A8, showing the slope and y-intercept of the line that best fits the data, as well as additional regression statistics if you included the optional third argument (“TRUE” or “1”).
Examples of LINEST function in Excel
Here are 10 examples of the LINEST function in Excel:
- Calculate a linear trendline for a set of data points:
=LINEST(B2:B7,A2:A7) - Calculate an exponential trendline for a set of data points:
=LINEST(B2:B7,LN(A2:A7),TRUE,TRUE) - Calculate a polynomial trendline of degree 2 for a set of data points:
=LINEST(B2:B7,A2:A7^{1,2}) - Calculate a multiple regression model with two independent variables for a set of data points:
=LINEST(B2:B7,A2:C7,{1,1,0},TRUE) - Calculate the slope and intercept of a linear trendline without displaying the array of coefficients:
=LINEST(B2:B7,A2:A7,,TRUE) - Calculate the standard error of the estimates for a linear trendline:
=STEYX(B2:B7,A2:A7) - Calculate the coefficient of determination for a linear trendline:
=RSQ(B2:B7,A2:A7) - Calculate the F statistic for a linear trendline:
=FISHER(LINEST(B2:B7,A2:A7))^(2*(COUNT(A2:A7)-2))/(1-RSQ(B2:B7,A2:A7)) - Calculate the confidence interval for the slope of a linear trendline:
=TINV(0.05,COUNT(A2:A7)-2)*STEYX(B2:B7,A2:A7)/SQRT(SUMSQ(A2:A7-(AVERAGE(A2:A7)))/COUNT(A2:A7)/(COUNT(A2:A7)-1)) - Calculate the predicted Y value for a given X value using a linear trendline:
=INDEX(LINEST(B2:B7,A2:A7),1)*X_VALUE+INDEX(LINEST(B2:B7,A2:A7),2)
How do you use LINEST function to calculate a regression line?
Let’s look at an example. Suppose you have a set of data that represents the relationship between two variables: x and y.
You want to find the best-fit line for this data using the LINEST function in Excel.
Here’s how you would use the LINEST function:
- Select a range of cells that correspond to the y-values in your data set.
- Enter the following formula in a blank cell: =LINEST(B2:B10, A2:A10, TRUE, TRUE) The first argument (B2:B10) represents the y-values in your data set. The second argument (A2:A10) represents the x-values in your data set. The third argument (TRUE) specifies that you want to include a constant term (y-intercept) in the regression equation. The fourth argument (TRUE) specifies that you want to return additional regression statistics along with the coefficients.
- Press Enter to calculate the regression coefficients and other statistics.
The LINEST function will return an array of values that represent the coefficients of the best-fit line. The first value represents the y-intercept, and the second value represents the slope.
To plot the regression line on a graph, you can use these coefficients to create an equation in the form y = mx + b, where m is the slope and b is the y-intercept.
Then, you can plot this equation on the same graph as your data points to visualize the best-fit line.
Can the LINEST function be used for multiple regression analysis?
Yes, the LINEST function in Excel can be used for multiple regression analysis.
Multiple regression analysis is a statistical technique that involves analyzing the relationship between a dependent variable and two or more independent variables.
To perform a multiple regression analysis in Excel, you need to enter your data into a table with columns for each of the independent variables and one column for the dependent variable. Here’s an example:
| Dependent Variable | Independent Variable 1 | Independent Variable 2 |
|---|---|---|
| 10 | 5 | 3 |
| 20 | 8 | 6 |
| 15 | 7 | 4 |
| 25 | 12 | 9 |
| 30 | 15 | 11 |
| 18 | 6 | 5 |
To use the LINEST function for multiple regression analysis on this data, you would select a range of cells that includes both the dependent and independent variable data (excluding headers), then enter the following formula:
=LINEST(A2:A7, B2:C7, TRUE, TRUE)
This will return an array of results that includes the intercept value, the slope coefficients for each independent variable, and various other statistics such as R-squared, standard error, and F-statistic.
You can use these results to interpret the regression equation and assess the strength of the relationship between the dependent variable and the independent variables.
Note that the LINEST function assumes a linear relationship between the dependent and independent variables. If your data suggests a non-linear relationship, you may need to use a different analytical method.
How to Fit a Polynomial Curve in Excel
To fit a polynomial curve in Excel, you can use the built-in functionalities of the program.
Here is a step-by-step guide:
Step 1: Prepare your data Organize your data into two columns in an Excel worksheet. The independent variable (x-values) should be listed in one column, and the dependent variable (y-values) should be listed in the adjacent column.
Step 2: Insert a scatter plot Select your data range, including both x and y values. Then go to the “Insert” tab on the Excel ribbon and choose “Scatter” under the “Charts” section. Select the scatter plot type that suits your preference.
Step 3: Add a trendline Right-click on any data point in the scatter plot and choose “Add Trendline” from the context menu. A “Format Trendline” pane will appear on the right side of the Excel window.
Step 4: Choose the polynomial order In the “Format Trendline” pane, select the “Polynomial” option. You will see a dropdown menu labeled “Order.” Choose the desired order for your polynomial curve. The order represents the degree of the polynomial (e.g., linear = 1, quadratic = 2, cubic = 3, etc.).
Step 5: Display equation and R-squared value Check the boxes labeled “Display Equation on Chart” and “Display R-squared Value” if you want Excel to show these values on your chart. The equation will represent the polynomial curve, and the R-squared value indicates the goodness-of-fit.
Step 6: Format the trendline You can customize the appearance of the trendline by adjusting various formatting options available in the “Format Trendline” pane. This includes line style, color, thickness, etc. Make the desired changes as per your preference.
Step 7: Analyze the results Review the displayed equation and R-squared value on the chart. The equation represents the polynomial curve that best fits your data, and the R-squared value indicates how well the curve fits the data points. Higher R-squared values indicate a better fit.
how to get the line of best fit with linest function
To get the line of best fit using the LINEST function in Excel, follow these steps:
- Enter your data points in two adjacent columns. For example, if your X-values are in column A and your Y-values are in column B, enter the values accordingly.
A B
1 X Y
2 1 3
3 2 5
4 3 7- In an empty cell, enter the following formula using the LINEST function:
=LINEST(B2:B4, A2:A4, TRUE, TRUE)- Press Enter to get the result. Excel will display an array of values corresponding to the line of best fit. The result will include multiple values such as the intercept, slope, standard error, etc. These values represent the equation for the line of best fit.
how to calculate the sum of squares using the LINEST function
The LINEST function is used to perform linear regression analysis, and it can also be used to calculate the sum of squares.
Assuming you have a set of x-values in column A and corresponding y-values in column B, you can follow these steps to calculate the sum of squares:
- In cell C2, enter the formula “
=LINEST(B2:B10, A2:A10^0)“. This formula calculates the linear regression for the data range B2:B10 against the powers of x in the range A2:A10. - Press Ctrl+Shift+Enter to enter the formula as an array formula. The result will appear as an array of values in cells C2:C3.
- In cell D2, enter the formula
=SUMSQ(B2:B10 - (C2*A2:A10^0 + C3)). This formula calculates the sum of squares by subtracting the predicted y-values (C2*A2:A10^0 + C3) from the actual y-values (B2:B10), squaring the differences, and then summing them up. - Cell D2 will display the sum of squares value for your data.
Here’s an example to illustrate this process:
| A | B | C | D |
|---|---|---|---|
| X | Y | Regression | Sum of Squares |
| ——- | ——- | ————- | —————– |
| 1 | 3 | 2.5 | 2.75 |
| 2 | 6 | 3.25 | 3.25 |
| 3 | 5 | 4 | 1 |
| 4 | 8 | 4.75 | 2.25 |
| 5 | 9 | 5.5 | 0.25 |
| 6 | 12 | 6.25 | 5.25 |
| 7 | 14 | 7 | 6.75 |
| 8 | 11 | 7.75 | 1.25 |
| 9 | 15 | 8.5 | 4.25 |
| ——- | ——- | ————- | —————– |
In the example above, columns C and D show the regression values and sum of squares, respectively, based on the LINEST function.
Remember to adjust the cell references (A2:A10 and B2:B10) according to your actual data range.
coefficient of determination with linest function
The LINEST function in Microsoft Excel is used to perform linear regression analysis and returns an array of values that can be used to calculate various statistics, including the coefficient of determination (R-squared).
To calculate the coefficient of determination using the LINEST function, you need to follow these steps:
Step 1: Enter your data
Enter the independent variable values (x-values) in one column and the corresponding dependent variable values (y-values) in another column.
Step 2: Use the LINEST function
In an empty cell, use the LINEST function to perform linear regression on the data. The syntax of the LINEST function is as follows:
=LINEST(known_y's, [known_x's], [const], [stats])Step 3: Retrieve the R-squared value (R2)
To get the coefficient of determination (R-squared), you need to extract the second element from the output array of the LINEST function.
The R-squared value represents the proportion of the variation in the dependent variable that can be explained by the independent variable(s).
Here’s an example formula that calculates the coefficient of determination using the LINEST function:
=INDEX(LINEST(B2:B10, A2:A10), 1, 2)^2In this example, B2:B10 represents the range of y-values, and A2:A10 represents the range of x-values.
The formula uses the INDEX function to extract the second element from the output array of LINEST, and then squares it to get the R-squared value.
Remember to adjust the cell references in the formula based on the location of your data in your Excel worksheet.
Note that the LINEST function assumes a simple linear regression model. If you’re working with multiple independent variables, you’ll need to modify the formula accordingly.
How do you interpret the output of the LINEST function?
The LINEST function is a built-in function in Excel that is used for linear regression analysis. It returns an array of values that describe the straight line that best fits the given data set, as well as statistics that can be used to assess the accuracy of the regression.
Now let’s look at an example to see how the LINEST function works and how to interpret its output.
Example: Suppose we have the following data set:
X Y 1 10 2 15 3 20 4 25 5 30
To find the equation of the line that best fits this data set, we can use the LINEST function as follows:
- Select a range of cells where you want to display the output of LINEST.
- Enter the following formula and press Ctrl+Shift+Enter to enter it as an array formula:
=LINEST(B2:B6,A2:A6,{1,TRUE})
This will return an array of five values corresponding to the coefficients of the regression line:
{5, 5}
This means that the equation of the line that best fits this data set is: y = 5x + 5.
The first value in the array (5) corresponds to the slope of the line (the change in y for a unit change in x), and the second value (5) corresponds to the y-intercept (the value of y when x is equal to 0).
If we want to see additional statistics, we can include the stats argument in the LINEST function. For example, if we want to see the R-squared value (a measure of how well the regression line fits the data), we can modify the formula as follows:
=LINEST(B2:B6,A2:A6,{1,TRUE},TRUE)
This will return an array of six values:
{5, 5, 1, 0, 0.98, 2.236}
The first four values are the same as before (slope, intercept, standard error of the slope, and standard error of the intercept).
The fifth value (0.98) is the R-squared value, which indicates that the regression line explains 98% of the variation in the data.
The sixth value (2.236) is the standard error of estimate, which measures the accuracy of the predicted y-values based on the regression equation.
how to find the slope of a line in excel
To find the slope of a line using the “LINEST” function in Excel, follow these steps:
- Enter your data points into two columns in Excel. For example, you can enter the x-values in column A and the corresponding y-values in column B.
- In an empty cell, type “=LINEST(y-values, x-values)” without the quotation marks. Replace “y-values” with the range of cells that contain your y-values, and “x-values” with the range of cells that contain your x-values. Make sure both ranges have the same number of data points. For example, if your y-values are in cells B2 to B10 and your x-values are in cells A2 to A10, the formula would be “=LINEST(B2:B10, A2:A10)“.
- Press Enter. Excel will calculate the slope and other statistical information related to the regression analysis.
- The result will appear as an array of values. The slope of the line is represented by the first value in the array.
Note: If you want to force the result to display only the slope, you can modify the formula by wrapping it in the “INDEX” function. For example, the modified formula would be “=INDEX(LINEST(B2:B10, A2:A10),1)“.
Remember to adjust the cell references according to the actual ranges of your data in your Excel worksheet.
What are the limitations of the LINEST function?
The LINEST function in Excel is a statistical function used to calculate the least-squares regression line that best fits two sets of data.
While it is a powerful tool, there are several limitations to the LINEST function that should be taken into consideration when using it.
- LINEST only works with linear relationships: The LINEST function assumes that there is a linear relationship between the two sets of data. If the relationship is not linear, then the results of the function may not be accurate. For example, if you have data that follows a curve or an exponential pattern, then the LINEST function will not be useful.
- LINEST requires equal length data sets: The two sets of data used by the LINEST function must have the same number of data points. If one set has more data points than the other, then the function will return an error. This means that you need to ensure that your data sets are properly aligned before using the function.
- LINEST can be affected by outliers: Outliers are data points that are far away from the rest of the data set. These data points can have a significant impact on the results of the LINEST function. They can skew the slope and intercept of the regression line and make it less accurate. It’s important to identify and remove any outliers before using the function.
- LINEST can’t handle missing data: If either of the two sets of data contains missing values, then the LINEST function will not work properly. You need to ensure that your data sets are complete before using the function.
- LINEST assumes independence of observations: The LINEST function assumes that each observation in one set of data is independent of the others. If there is any dependency between the observations, then the function may not provide accurate results.
Example:
Suppose you have two sets of data, X and Y, representing the number of hours studied and the corresponding test scores for a group of students.
You want to use the LINEST function to find the equation of the regression line that best fits the data.
However, if the relationship between studying hours and test scores is not linear or there are outliers present in the data, the LINEST function may provide inaccurate results.
Therefore, you should always evaluate the assumptions and limitations of the LINEST function before using it.
Can the LINEST function handle missing data?
The LINEST function in Excel is used to calculate the statistics of a trendline that best fits a given set of data points. This function can handle missing data, but its behavior varies depending on how the missing data is treated.
When using the LINEST function, missing data can be handled either by ignoring it or by treating it as zero.
The default behavior of the function is to ignore any missing data in the input range, which means that the corresponding data points are excluded from the regression analysis.
However, if you want to include the missing data in the analysis, you can do so by specifying the optional argument “TRUE” for the const input parameter.
This will cause the missing data to be treated as zero and included in the calculation of the regression coefficients.
Let’s take an example to understand this better. Suppose we have the following data set:
| X | Y |
|---|---|
| 1 | 15 |
| 2 | |
| 3 | 21 |
| 4 | 27 |
| 5 | 35 |
In this data set, there is a missing value for Y at X=2. If we want to calculate the regression coefficients for this data set using the LINEST function, we can use the following formula:
=LINEST(B2:B6,A2:A6,,TRUE)
The first two arguments (B2:B6 and A2:A6) represent the Y and X values respectively. The third argument is left empty because we don’t need to specify any additional information.
The fourth argument (TRUE) tells the LINEST function to treat missing data as zero.
The output of this formula will be an array containing the slope, y-intercept, correlation coefficient, standard error of the slope, and standard error of the y-intercept, in that order:
{7.3, 8.2, 0.985, 1.3, 3.0}
Note that the LINEST function has treated the missing value at X=2 as zero, which has affected the regression coefficients.
In conclusion, the LINEST function in Excel can handle missing data by either ignoring it or treating it as zero, depending on the optional arguments used.
How accurate are the results obtained from the LINEST function?
The LINEST function in Excel is used for linear regression analysis, which is a statistical method for determining the relationship between two variables.
It calculates the coefficients of a linear equation that best fits a set of data points.
The results obtained from the LINEST function are generally accurate if the assumptions of linear regression are met.
These assumptions include linearity, independence, normality, and equal variance. If these assumptions are violated, the results may not be accurate or meaningful.
To demonstrate the use of the LINEST function and its accuracy, consider the following example:
Suppose we have a dataset of 10 observations with two variables, x and y, and we want to determine the coefficient of the linear equation that best fits the data.
We can use the LINEST function in Excel to calculate the coefficients as follows:
- Enter the values of x and y in two columns in Excel.
- Select an empty cell in the worksheet where you want to display the results.
- Type “=LINEST(y-range, x-range, TRUE, TRUE)” into the formula bar, where “y-range” is the range of cells containing the y-values and “x-range” is the range of cells containing the x-values.
- Press Enter to calculate the coefficients.
Excel will return an array of values, including the intercept, slope, and other statistics related to the linear regression. The accuracy of these results depends on whether the assumptions of linear regression are met.
For example, if the data points exhibit a clear linear relationship, the LINEST function will produce accurate results.
However, if the data points are scattered randomly with no clear pattern, the LINEST function may produce inaccurate results.
In conclusion, the accuracy of the LINEST function in Excel depends on whether the assumptions of linear regression are met.
Therefore, it is important to understand the underlying assumptions and interpret the results accordingly.
What is the difference between the LINEST and the LOGEST functions?
Both LINEST and LOGEST are Excel functions that can be used to calculate linear regression equations for a set of data points.
However, there is one key difference between the two: LINEST is used for linear regression, while LOGEST is used for exponential regression.
Linear regression involves finding the line of best fit for a set of data points, while exponential regression involves finding the curve of best fit for a set of data points.
Here are some examples to demonstrate the difference:
Example 1 – Linear Regression Using LINEST: Suppose we have the following table of data:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
| 5 | 10 |
To perform linear regression using LINEST, we would enter the following formula into a cell:
=LINEST(y-values, x-values, TRUE, TRUE)
In this case, the “y-values” are the dependent variable (the values we are trying to predict), and the “x-values” are the independent variable (the values we are using to make the predictions).
The last two arguments, TRUE and TRUE, tell Excel to return additional statistical information about the regression, such as the R-squared value and the standard error.
The output of the LINEST function would be an array of coefficients that define the line of best fit for the data. In this case, the coefficients would be:
| m |
|---|
| 2 |
| 0 |
This means that the equation for the line of best fit is y = 2x + 0. We can use this equation to make predictions about future data points based on their x-values.
Example 2 – Exponential Regression Using LOGEST: Suppose we have the following table of data:
| x | y |
|---|---|
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
To perform exponential regression using LOGEST, we would first need to take the natural logarithm of both the x and y values. We can do this using the LN function in Excel:
| ln(x) | ln(y) |
|---|---|
| 0 | 0.693147 |
| 0.693147 | 1.386294 |
| 1.098612 | 2.079442 |
| 1.386294 | 2.772589 |
| 1.609438 | 3.465736 |
We can then enter the following formula into a cell to perform exponential regression using LOGEST:
=LOGEST(ln(y-values), ln(x-values), TRUE, TRUE)
In this case, the “y-values” are still the dependent variable, but they are now the natural logarithms of the actual y-values. The “x-values” are still the independent variable, but they are now the natural logarithms of the actual x-values.
The output of the LOGEST function would be an array of coefficients that define the curve of best fit for the data. In this case, the coefficients would be:
| m | b |
|---|---|
| 2.1563 | 0.4022 |
This means that the equation for the curve of best fit is y = e^(2.1563*ln(x) + 0.4022). We can use this equation to make predictions about future data points based on their x-values.
So to summarize, LINEST is used for linear regression, while LOGEST is used for exponential regression. LINEST calculates the line of best fit for a set of data points, while LOGEST calculates the curve of best fit for a set of data points.