What is LOGNORM.INV function in Excel?
The LOGNORM.INV function is one of the Statistical functions of Excel.
It returns the inverse of the lognormal cumulative distribution function of x where ln(x) is normally distributed with parameters Mean and Standard_dev.
We can find this function in Statistical of insert function Tab.
How to use LOGNORM.INV function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
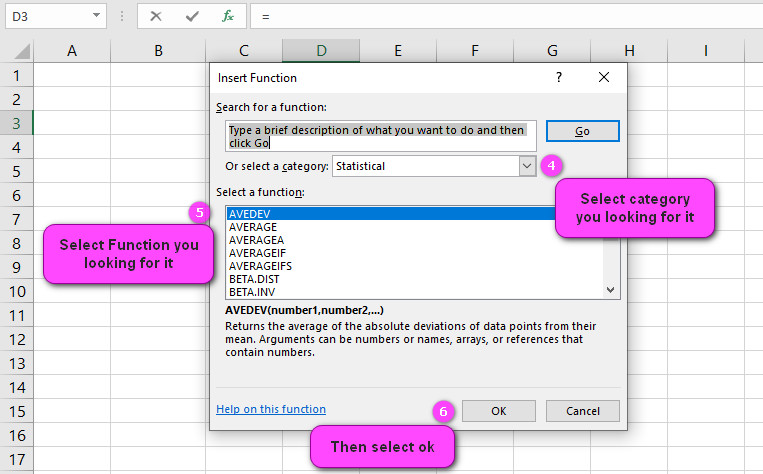
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select LOGNORM.INV function.
6. Then select ok.
7. In the function arguments Tab you will see LOGNORM.INV function.
8. Probability is a probability associated with the lognormal distribution, a number
between 0 and 1, inclusive.
9. Mean is the mean of ln(x).
10. Standard_dev is the standard deviation of ln(x), a positive number.
11. You will see the results in the formula result section.
What is LOGNORM.INV function in Excel?
The LOGNORM.INV function in Excel is a statistical function that returns the inverse of the cumulative normal distribution for a specified mean and standard deviation of a logarithmic normal distribution.
In other words, it calculates the value x such that the cumulative distribution function of the logarithmic normal distribution at x is equal to a specified probability.
The syntax for the LOGNORM.INV function is as follows:
=LOGNORM.INV(probability, mean, standard_dev)
where:
probabilityis the probability for which you want to find the inverse of the cumulative distribution.meanis the arithmetic mean (average) of the logarithm of the distribution.standard_devis the standard deviation of the logarithm of the distribution.
Now, let’s take an example to understand how the LOGNORM.INV function works:
Suppose we have a set of data that follows a logarithmic normal distribution with a mean of 2 and a standard deviation of 0.5.
We want to find out the value corresponding to a cumulative distribution of 0.75.
To do this, we can use the following formula:
=LOGNORM.INV(0.75, 2, 0.5)
This will return the value of 3.1472, which represents the value at which the cumulative distribution of the logarithmic normal distribution is equal to 0.75, given the specified mean and standard deviation.
In summary, the LOGNORM.INV function in Excel is a powerful statistical tool that can be used to calculate the inverse of the cumulative distribution for a logarithmic normal distribution.
It is particularly useful in financial analysis and modeling, where logarithmic normal distributions are commonly used to model asset returns and prices.
What are the arguments for the LOGNORM.INV Function?
The LOGNORM.INV function in Excel returns the inverse of the cumulative distribution function (CDF) for a specified lognormal distribution. The function takes four arguments:
- Probability: This is the probability for which you want to calculate the inverse of the CDF. It must be between 0 and 1.
- Mean: This is the mean of the lognormal distribution.
- Standard deviation: This is the standard deviation of the lognormal distribution.
- Cumulative: This is a logical value that determines the form of the function. If it is TRUE or omitted, the function returns the cumulative distribution function; if it is FALSE, the function returns the probability density function.
The syntax for the function is as follows:
=LOGNORM.INV(Probability, Mean, Standard_dev,[Cumulative])
Here’s an example that demonstrates the usage of the LOGNORM.INV function:
Suppose we have a lognormal distribution with a mean of 5 and a standard deviation of 1.5. We want to find the value x such that P(X <= x) = 0.75. To do this, we can use the following formula in Excel:
=LOGNORM.INV(0.75, 5, 1.5, TRUE)
The result of this formula is 6.406. This means that there is a 75% chance that a random variable drawn from this lognormal distribution will be less than or equal to 6.406.
In another example, suppose we have a similar lognormal distribution but we want to find the probability density function at a specific point.
Let’s say we want to find the value of the PDF at x = 7. To do this, we can use the following formula in Excel:
=LOGNORM.INV(7, 5, 1.5, FALSE)
The result of this formula is 0.107. This means that the probability density at x = 7 is 0.107.
How does the LOGNORM.INV Function work?
The LOGNORM.INV function in Excel returns the inverse of the cumulative distribution function (CDF) of a lognormal distribution.
In other words, given a probability value between 0 and 1, it returns the corresponding value from a lognormal distribution.
The syntax for the LOGNORM.INV function is as follows:
=LOGNORM.INV(probability, [mean], [standard_dev])
where:
- Probability is the probability value for which you want to find the corresponding value of the lognormal distribution.
- Mean (optional) is the mean of the logarithm of the distribution. If omitted, the default value is 0.
- Standard_dev (optional) is the standard deviation of the logarithm of the distribution. If omitted, the default value is 1.
Here’s an example. Suppose you have a lognormally distributed set of data with a mean of 10 and a standard deviation of 2. You want to find the value that corresponds to a probability of 0.95. To do this, you can use the following formula:
=LOGNORM.INV(0.95, 10, 2)
The result of this formula would be approximately 19.03. This means that there is a 95% chance that a randomly selected value from the lognormal distribution would be less than or equal to 19.03.
Another example is if you wanted to find the value that corresponds to a more extreme probability, say 0.001.
Using the same mean and standard deviation values as before, you can use the following formula:
=LOGNORM.INV(0.001, 10, 2)
The result of this formula would be approximately 3.75. This means that there is only a 0.1% chance that a randomly selected value from the lognormal distribution would be less than or equal to 3.75.
What is the syntax for the LOGNORM.INV Function?
The syntax for the LOGNORM.INV function in Excel is:
=LOGNORM.INV(probability, mean, standard_dev)
where:
probabilityis the probability of the log-normal distributionmeanis the arithmetic mean of the logarithm of the distributionstandard_devis the standard deviation of the logarithm of the distribution
The LOGNORM.INV function returns the inverse of the log-normal cumulative distribution function for a specified probability value.
In other words, it calculates the value that corresponds to a given probability in a log-normal distribution.
Here’s an example of how to use the LOGNORM.INV function in Excel:
Suppose we have a log-normal distribution with a mean of 10 and a standard deviation of 0.5. We want to find the value that corresponds to a probability of 0.9. We can use the LOGNORM.INV function as follows:
=LOGNORM.INV(0.9, 10, 0.5)
This will return the value 14.112, which is the value that corresponds to a probability of 0.9 in our log-normal distribution with a mean of 10 and a standard deviation of 0.5.
Note that because the LOGNORM.INV function assumes a log-normal distribution, the mean and standard deviation parameters should be based on the logarithm of the data.
If you have data that is not already in logarithmic form, you may need to transform it first using the LN function in Excel.
How do I use the LOGNORM.INV Function to calculate a percentile?
The LOGNORM.INV function in Excel is used to calculate the inverse of the cumulative distribution function for a lognormal distribution.
This function can be used to find the value at a given percentile based on the parameters of the distribution.
The syntax of the LOGNORM.INV function is:
=LOGNORM.INV(probability, mean, standard_dev)
Where:
- probability: The probability for which you want to find the corresponding value.
- mean: The arithmetic mean of the lognormal distribution.
- standard_dev: The standard deviation of the lognormal distribution.
To use the function to calculate a percentile, you need to provide a known probability and the mean and standard deviation of the lognormal distribution. Here is an example:
Suppose we have a set of data that follows a lognormal distribution with a mean of 10 and a standard deviation of 1.5. We want to find the value at the 75th percentile of this distribution.
To do this using the LOGNORM.INV function, we can enter the following formula into a cell:
=LOGNORM.INV(0.75, 10, 1.5)
This will return the value 13.7386, which represents the value at the 75th percentile of the lognormal distribution.
Another example: Suppose we have a set of data that follows a lognormal distribution with a mean of 8 and a standard deviation of 2. We want to find the value at the 90th percentile of this distribution.
To do this using the LOGNORM.INV function, we can enter the following formula into a cell:
=LOGNORM.INV(0.90, 8, 2)
This will return the value 14.2839, which represents the value at the 90th percentile of the lognormal distribution.
Can the LOGNORM.INV Function be used for non-normal distributions?
The LOGNORM.INV function in Excel is used to calculate the inverse of the logarithmic normal cumulative distribution.
It can be used for any continuous probability distribution that has a well-defined inverse cumulative distribution function (also known as the quantile function).
However, it is important to note that while the function itself is designed to model a specific type of distribution (log-normal), it can still be used to approximate other distributions with similar characteristics.
For example, suppose you have a set of data that represents the time it takes for customers to complete a certain task on your website.
If you plot this data on a histogram or density plot, and it resembles a log-normal distribution, then you could use the LOGNORM.INV function to generate random values from that distribution.
Here’s an example of how you might use the LOGNORM.INV function in Excel:
Suppose you want to generate 100 random values from a log-normal distribution with a mean of 10 and a standard deviation of 2. You could use the following formula:
=LOGNORM.INV(RAND(), LN(10), LN(2))
This formula will generate a random value from the log-normal distribution at a probability equal to a random number generated by the RAND function.
Note that we pass the natural logarithm of the mean and standard deviation to the function, which is required by the function.
In summary, while the LOGNORM.INV function is specifically designed to model log-normal distributions, it can still be used to approximate other distributions as long as they have a well-defined inverse cumulative distribution function.
What is the difference between the LOGNORM.INV and NORM.INV Functions?
Both the LOGNORM.INV and NORM.INV functions are used in Excel to determine the inverse of a cumulative normal distribution.
However, the difference between the two lies in the type of distribution being used.
The NORM.INV function calculates the inverse of a standard normal distribution with a mean of 0 and a standard deviation of 1.
This means that if you have a normally distributed set of data with a known mean and standard deviation, you can use the NORM.INV function to calculate the value corresponding to a specific probability level.
For example, let’s say you have a normally distributed data set with a mean of 50 and a standard deviation of 10.
You want to know the value that corresponds to a probability level of 0.95. Using the NORM.INV function, you would input “=NORM.INV(0.95,50,10)” into an Excel cell, which would return the value of approximately 69.13.
On the other hand, the LOGNORM.INV function calculates the inverse of a lognormal distribution, where the natural logarithm of the data is normally distributed.
This is useful when dealing with data that has a skewed distribution, such as financial data.
For example, let’s say you have a set of financial data that is lognormally distributed with a mean of 5 and a standard deviation of 2.
You want to know the value that corresponds to a probability level of 0.90. Using the LOGNORM.INV function, you would input “=LOGNORM.INV(0.90,5,2)” into an Excel cell, which would return the value of approximately 24.47.
In summary, both NORM.INV and LOGNORM.INV are used to calculate the inverse of a cumulative normal distribution, but NORM.INV is used for a standard normal distribution while LOGNORM.INV is used for a lognormal distribution.
How do I input data into the LOGNORM.INV Function?
Here’s how to input data into the function:
- Probability: This is the probability value between 0 and 1 for which you want to determine the corresponding inverse lognormal distribution value. It must be entered as a decimal number. For example, if you want to find the inverse lognormal distribution value for a probability of 0.5 (or 50%), you would enter 0.5.
- Mean: This is the arithmetic mean of the natural logarithm of the random variable. It must be entered as a positive number. For example, if your sample data has a mean of 2.5, you would enter 2.5.
- Standard deviation: This is the standard deviation of the natural logarithm of the random variable. It must be entered as a positive number. For example, if your sample data has a standard deviation of 0.5, you would enter 0.5.
- Cumulative (optional): This is an optional logical value that determines which form of the function you want to use. If this argument is omitted or set to TRUE, the function returns the cumulative distribution function; if it is FALSE, the function returns the probability density function.
Here’s an example of the function using these inputs:
=LOGNORM.INV(0.25, 2.5, 0.5)
This function calculates the inverse of the lognormal cumulative distribution function for a random variable with a mean of 2.5 and a standard deviation of 0.5, for a probability of 0.25.
The function returns the corresponding inverse lognormal distribution value.
Note that if you include the optional argument and set it to FALSE, the function will return the probability density function instead of the cumulative distribution function.
What are some common mistakes when using the LOGNORM.INV Function?
The LOGNORM.INV function in Excel is used to calculate the inverse of the cumulative distribution function (CDF) of the lognormal distribution.
This function can be useful for financial and statistical analysis, but it is important to use it correctly in order to get accurate results.
Here are some common mistakes that people make when using the LOGNORM.INV function in Excel:
- Forgetting to enter the parameters in the correct order: The LOGNORM.INV function takes three parameters: probability, mean, and standard deviation. If you enter these parameters in the wrong order, you will get an incorrect result. Make sure to enter them in the correct order.
- Using the wrong type of mean or standard deviation: The LOGNORM.INV function requires a natural logarithmic mean and standard deviation, not the arithmetic mean and standard deviation. If you use the wrong type of mean or standard deviation, your results will be inaccurate. You can convert from arithmetic to logarithmic mean and standard deviation using the LN function.
- Not specifying a probability value: The probability parameter in the LOGNORM.INV function specifies the percentile of the distribution that you want to find. If you do not specify a probability value, the function will not know what percentile to calculate and will return an error.
- Using a probability value outside the range of 0 to 1: The probability parameter in the LOGNORM.INV function must be between 0 and 1. If you use a probability value outside of this range, you will get an error.
Here is an example of how to use the LOGNORM.INV function correctly:
Suppose we want to find the value of x such that the lognormal distribution with a mean of 10 and a standard deviation of 2 has a cumulative distribution value of 0.75. We can use the following formula:
=LOGNORM.INV(0.75, LN(10), LN(2))
In this example, we have specified the probability value of 0.75, the natural logarithmic mean of 10 (which is calculated using the LN function), and the natural logarithmic standard deviation of 2 (also calculated using the LN function). The result of this formula is approximately 13.5.
How can I verify if my LOGNORM.INV calculations are correct?
LOGNORM.INV is an Excel function that calculates the inverse of the cumulative distribution function (CDF) for a log-normal distribution.
This function can be used to find the value of x at which the cumulative log-normal distribution equals a given probability value.
To verify your LOGNORM.INV calculations in Excel, you can follow these steps:
- Generate a set of random data that follows a log-normal distribution using the RAND and LOGNORM.INV functions.
For example, enter the following formula into cell A2:
=RAND()
Then, enter this formula into cell B2:
=LOGNORM.INV(A2, 1, 0.5)
This will generate a random number between 0 and 1 in cell A2 and use it as the probability value for the LOGNORM.INV function with a mean of 1 and a standard deviation of 0.5.
Copy and paste these formulas down the column to generate more data points.
- Calculate the actual probability value for each data point using the LOGNORM.DIST function.
Enter the following formula into cell C2:
=LOGNORM.DIST(B2, 1, 0.5, TRUE)
This will calculate the cumulative distribution function (CDF) for a log-normal distribution with a mean of 1 and a standard deviation of 0.5 at the value in cell B2.
Copy and paste this formula down the column to calculate the actual probability value for each data point.
- Create a scatter plot of the generated data.
Select the data in columns A, B, and C, and go to Insert > Charts > Scatter, and choose a scatter plot.
- Add a reference line for the desired probability value.
Right-click on the chart, choose “Select Data”, and then click “Add” to add a new series. Enter the desired probability value in the “Series values” box (e.g. 0.5 for a probability of 50%), and then choose the same x-values as your data.
Format this new series to be a line with a different color or style than your data points.
- Compare the actual values to the reference line.
If the LOGNORM.INV function is working correctly, the generated data points should lie on the reference line for the desired probability value. If the points are consistently above or below the line, there may be an error in your calculations.
Note that this method only verifies the accuracy of the computed probabilities, not the correctness of the LOGNORM.INV formula itself. To verify the formula, you can compare its output to a known set of values or use a different software package to compute the inverse log-normal CDF.
Examples of LOGNORM.INV function in Excel
here are 10 examples of using the LOGNORM.INV function in Excel:
- To find the value that corresponds to a given probability of occurrence for a lognormal distribution with a specified mean and standard deviation:
=LOGNORM.INV(0.5, 2, 0.5)
- To calculate the inverse cumulative distribution function for a lognormal distribution with a mean of 3 and a standard deviation of 1.5 at the 90th percentile:
=LOGNORM.INV(0.9, 3, 1.5)
- To calculate the value that represents the 95th percentile of a lognormal distribution with a mean of 4 and a standard deviation of 2:
=LOGNORM.INV(0.95, 4, 2)
- To determine the value that is exceeded by a given percentage of observations for a lognormal distribution with a mean of 5 and a standard deviation of 0.75:
-
=LOGNORM.INV(0.2, 5, 0.75)
-
- To calculate the inverse cumulative distribution function for a lognormal distribution with a mean of 1.5 and a standard deviation of 0.5 at the 80th percentile:
=LOGNORM.INV(0.8, 1.5, 0.5)
- To find the value at which 75% of the data is below it for a lognormal distribution with a mean of 2 and a standard deviation of 1.2:
=LOGNORM.INV(0.75, 2, 1.2)
- To determine the value that corresponds to a given probability of occurrence for a lognormal distribution with a mean of 3.5 and a standard deviation of 1:
-
=LOGNORM.INV(0.4, 3.5, 1)
-
- To calculate the inverse cumulative distribution function for a lognormal distribution with a mean of 2 and a standard deviation of 0.8 at the 70th percentile:
=LOGNORM.INV(0.7, 2, 0.8)
- To find the value that represents the 60th percentile of a lognormal distribution with a mean of 1 and a standard deviation of 0.5:
=LOGNORM.INV(0.6, 1, 0.5)
- To determine the value that is exceeded by 90% of observations for a lognormal distribution with a mean of 4.5 and a standard deviation of 1.5:
=LOGNORM.INV(0.1, 4.5, 1.5)