What is SIN function in Excel?
The SIN function is one of the math functions of Excel.
It Returns the sine of an angle.
We can find this function in Math & trig category of insert function Tab.
How to use SIN function in excel
- Click on an empty cell (like F5 )
2. Click on fx icon (or press shift+F3)
3. In the insert function tab you will see all functions
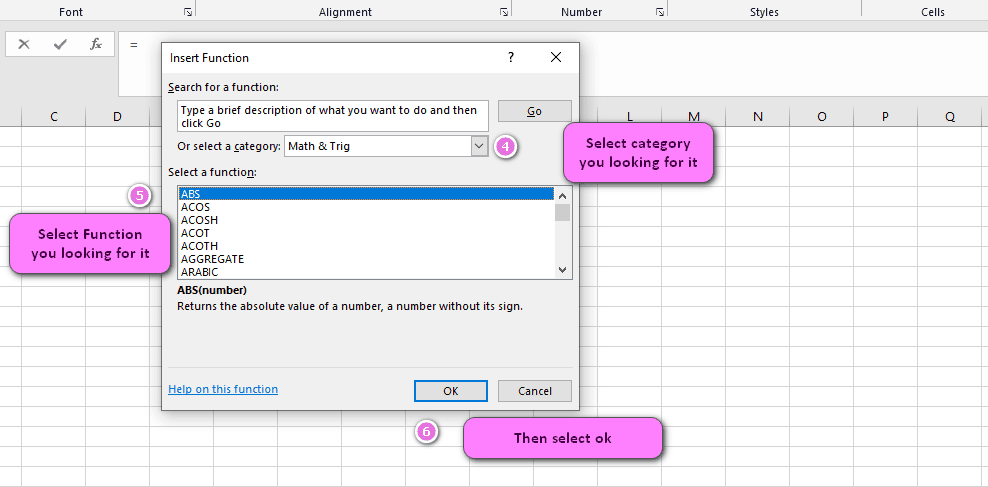
4. Select math and trig category
5. Select SIN function
6. Then select ok
7. In the function arguments Tab you will see SIN function
8. Number is the angle in radians for which you want the sine. Degrees * P10/180 = radians
9. You will see results in the formula result section

Examples of SIN function in Excel
=SIN(0)returns 0, since the sine of 0 radians is 0.=SIN(1)returns 0.841471, which is the sine of 1 radian.=SIN(PI())returns 0, since the sine of π radians (180 degrees) is 0.=SIN(RADIANS(45))returns 0.707107, which is the sine of 45 degrees converted to radians.=SIN(A2)returns the sine of the value in cell A2.=SIN(2*PI()*A2)returns the sine of the value in cell A2 when it is interpreted as an angle in radians.=SIN(-1)returns -0.841471, which is the sine of -1 radian.=SIN(A1+A2)returns the sine of the sum of the values in cells A1 and A2.=SIN(SUM(A1:A10))returns the sine of the sum of the values in cells A1 through A10.=SIN(IF(A1>0, A2, A3))returns the sine of the value in cell A2 if the value in cell A1 is greater than zero, otherwise it returns the sine of the value in cell A3.
Example 1:
How to use SIN function in excel
You can see examples of SIN function below:

sin(A2) ----->>>>answer is 0
sin(A3) ----->>>>answer is 0.70
sin(A4) ----->>>>answer is -1
sin(A5) ----->>>>answer is -0.86
sin(A6) ----->>>>answer is 0Excel’s SIN function: What it is and how to use it effectively
Excel’s SIN function is a mathematical function that returns the sine of an angle. The function takes one argument, which can be in radians or degrees, and returns a value between -1 and 1.
For example, if you want to calculate the sine of 45 degrees, you would use the following formula:
=SIN(RADIANS(45))
This formula converts 45 degrees to radians using the RADIANS function and then calculates the sine of the resulting angle using the SIN function.
Mastering the SIN function in Excel: Tips and tricks for accurate results
To master the SIN function in Excel, there are several tips and tricks to keep in mind. These include:
- Convert angles to radians using the RADIANS function before using the SIN function.
- Be sure to use the correct units (radians or degrees) when inputting arguments into the SIN function.
- Handle non-numeric or empty cell inputs appropriately using the IFERROR function or other techniques.
- Combine the SIN function with other functions or operators for more advanced calculations.
- Use conditional statements like IF or SWITCH to control the output of the SIN function based on certain conditions.
By following these tips and tricks, users can ensure accurate results when working with the SIN function in Excel.
Exploring the arguments and values of Excel’s SIN function
The SIN function in Excel takes one argument, which is the angle whose sine is to be calculated. This argument can either be in radians or degrees, depending on the needs of the calculation.
For example, if you wanted to calculate the sine of 30 degrees, you could use the following formula:
=SIN(RADIANS(30))
This formula converts 30 degrees to radians using the RADIANS function and then calculates the sine of the resulting angle using the SIN function.
How Excel’s SIN function calculates sine values
The SIN function in Excel calculates the sine of an angle using a mathematical algorithm based on the Taylor series expansion. This algorithm provides an approximate value for the sine of an angle by adding up a series of terms with decreasing magnitudes.
For example, if you wanted to calculate the sine of 1 radian using this algorithm, you would use the following formula:
=SIN(1)
This formula returns approximately 0.84147, which is the sine of 1 radian calculated using the Taylor series expansion.
Excel’s SIN function: Handling angles in degrees and radians
Excel’s SIN function can handle angles in both degrees and radians, but it is important to use the correct units when inputting arguments into the function. If the argument is in degrees, it must be converted to radians before being used in the SIN function.
For example, if you wanted to calculate the sine of 45 degrees, you could use the following formula:
=SIN(RADIANS(45))What happens when an empty cell is used as an argument for Excel’s SIN function?
If an empty cell is used as an argument for Excel’s SIN function, the function will return a #VALUE! error. This error occurs because the SIN function requires a numeric argument to calculate the sine of an angle.
For example, if you had an empty cell A1 and tried to calculate the sine of its value using the following formula:
=SIN(A1)
Excel would return a #VALUE! error.
Converting degrees to radians for use with Excel’s SIN function
Excel’s SIN function requires arguments in radians, so it is often necessary to convert degrees to radians before using the function. This can be done using the RADIANS function in Excel.
For example, if you wanted to calculate the sine of 30 degrees, you would use the following formula:
=SIN(RADIANS(30))
This formula converts 30 degrees to radians using the RADIANS function and then calculates the sine of the resulting angle using the SIN function.
Understanding the difference between Excel’s SIN and ASIN functions
The SIN and ASIN functions in Excel are both trigonometric functions, but they have different purposes. The SIN function returns the sine of an angle, while the ASIN function returns the arcsine of a value.
For example, if you wanted to calculate the arcsine of 0.5, you would use the following formula:
=ASIN(0.5)
This formula would return the angle whose sine is 0.5, which is approximately 0.5236 radians or 30 degrees.
Combining Excel’s SIN function with mathematical and logical operators
Excel’s SIN function can be combined with other mathematical and logical operators to perform more advanced calculations. For example, you could use the SIN function in a formula to calculate the hypotenuse of a right triangle:
=SQRT(SIN(A1)^2 + COS(A1)^2)
This formula uses the SIN and COS functions to calculate the length of the sides of a right triangle, and then uses the SQRT function to find the square root of the sum of their squares, which is the length of the hypotenuse.
Using conditional statements with Excel’s SIN function: Examples and best practices
Conditional statements like IF or SWITCH can be used to control the output of the SIN function based on certain conditions. For example, you could use an IF statement to return different results depending on whether the sine of an angle is positive or negative:
=IF(SIN(A1)>0, "Positive", "Negative")
This formula returns the text “Positive” if the sine of the value in cell A1 is greater than zero, and “Negative” if it is less than zero.
Formatting the result of Excel’s SIN function for enhanced data visualization
The result of Excel’s SIN function can be formatted using various tools and techniques to enhance its visual appearance. For example, you could apply a custom number format to make the result appear as a percentage:
=SIN(A1)*100
You could then apply a custom number format like “0.00%” to display the result as a percentage with two decimal places.
Navigating limitations and restrictions when using Excel’s SIN function
Like any mathematical function, Excel’s SIN function has certain limitations and restrictions that must be navigated when using it in calculations. These may include issues related to input values outside the valid range, accuracy and precision of results, and computational speed and efficiency.
For example, if you tried to calculate the sine of an angle that was extremely large or small, the SIN function might return an error or incorrect result due to floating point precision issues.
Combining Excel’s SIN function with other functions for advanced data analysis
Excel’s SIN function can be combined with other functions and operators in complex formulas for advanced data analysis tasks. For example, you could use the SIN function in a formula to simulate a sound wave:
=SIN(2*PI()*A1*440)+SIN(2*PI()*A1*880)
This formula uses the SIN function twice to create two sine waves at frequencies of 440 Hz and 880 Hz, respectively. It then adds these waves together to create a more complex waveform.
Utilizing Excel’s SIN function for creating sine wave graphs
Excel’s SIN function can be used to create sine wave graphs for visualization and analysis purposes. To do this, you would need to generate a series of angles at regular intervals and calculate their sines using the SIN function. You could then plot these angles and sines on a graph to create a wave pattern.
For example, you could use the following formula to generate a sine wave with a frequency of 1 Hz and plot it on a graph:
=SIN(2*PI()*A1)Excel’s SIN function and trigonometric identities: Applications and examples
Excel’s SIN function can be used to calculate various trigonometric identities, including the Pythagorean identity:
=SIN(A1)^2 + COS(A1)^2
This formula calculates the sum of the squares of the sine and cosine of an angle, which is always equal to 1 according to the Pythagorean identity.
Calculating the inverse sine function using Excel’s SIN function
The inverse sine, or arcsine, function can be calculated using the SIN function in Excel. The formula for calculating the arcsine of a value is:
=ASIN(SIN(A1))
This formula returns the angle whose sine is equal to the value in cell A1.
Using Excel’s SIN function to calculate the height of a triangle
Excel’s SIN function can be used to calculate the height of a triangle given its base length and an angle opposite the base. The formula for calculating the height is:
=BASE_LENGTH*SIN(ANGLE)
For example, if you had a triangle with a base length of 10 meters and an angle opposite the base of 30 degrees, you could use the following formula to calculate the height:
=10*SIN(RADIANS(30))
This formula converts 30 degrees to radians using the RADIANS function and then calculates the sine of the resulting angle using the SIN function. The result would be approximately 5 meters, which is the height of the triangle.
Experts weigh in on common issues and troubleshooting techniques for Excel’s SIN function
Common issues and troubleshooting techniques for Excel’s SIN function include:
- Be sure to convert angles to radians before inputting them into the SIN function.
- Handle non-numeric or empty cell inputs using the IFERROR function or other techniques.
- Use conditional statements like IF or SWITCH to control the output of the SIN function based on certain conditions.
- Be aware of floating point precision issues when working with extremely large or small values in the SIN function.
- Consider combining the SIN function with other functions or operators for more advanced calculations.
Experts also recommend testing formulas using known inputs and comparing the results to expected outputs to quickly identify issues and errors.

