Excel Degrees Function

What is Degrees Function in Excel?

The Degrees function is one of the math functions of Excel.

It Converts radiants to degrees.

We can find this function in Math&trig category of insert function Tab.

How to use Degrees function in excel

1. Click on an empty cell (like F5 )

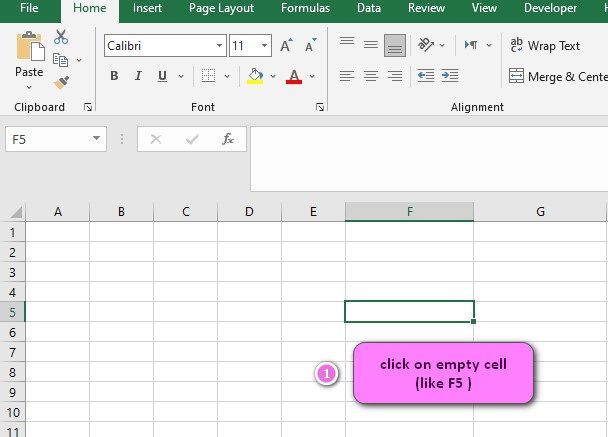
2. Click on fx icon (or press shift+F3)

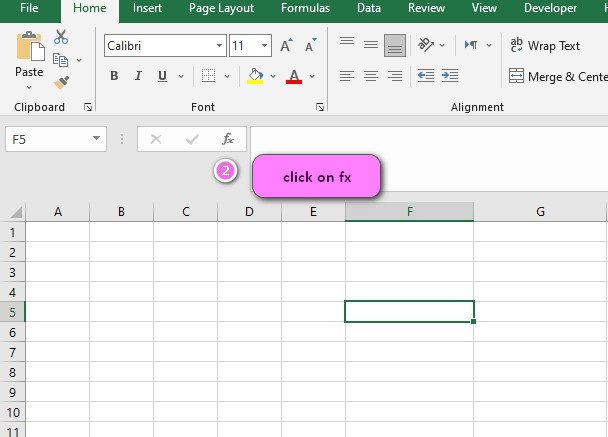
3. In the insert function tab you will see all functions

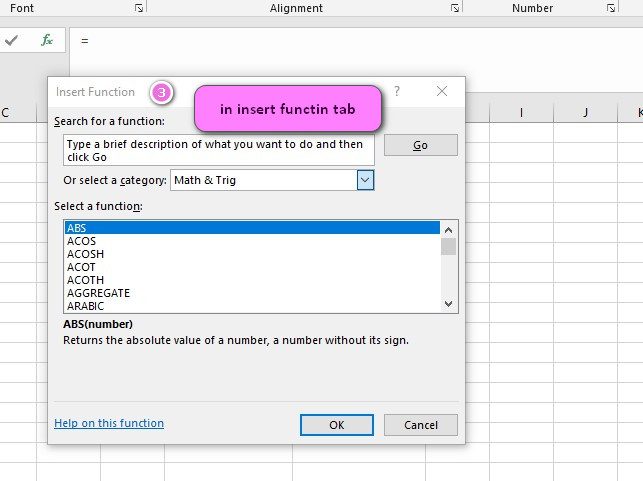
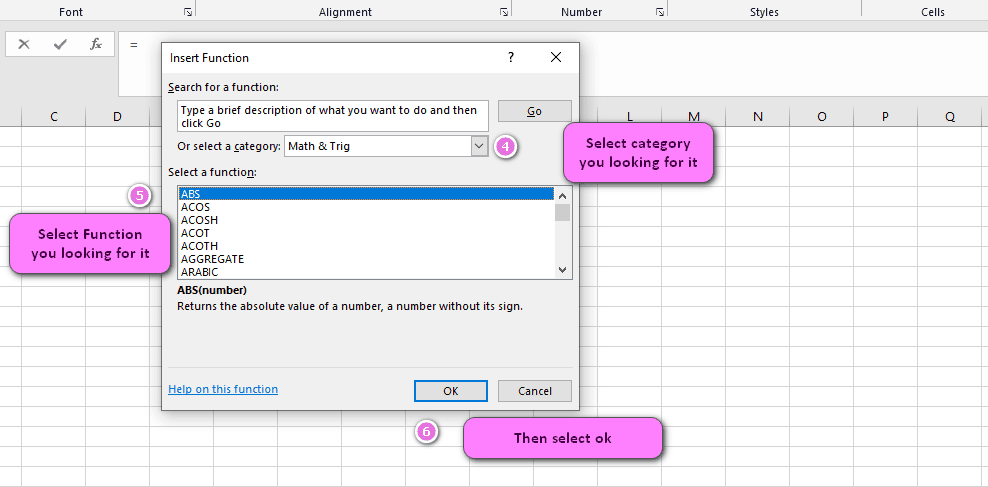
4. Select math and trig category

5. Select Degrees function

6. Then select ok

7. In the function Arguments Tab you will see Degrees function

8. Angle is the angle in radians that you want to convert for example : pi()

9. You will see results in the formula result section

Examples of Degrees function in Excel

1. Convert radians to degrees: =DEGREES(3.14159/2) This formula would return a result of 90 degrees, which is equal to pi/2 radians.
2. Convert angle in decimal degrees to degrees, minutes, and seconds: =TEXT(DEGREES(0.5236),”0°00’00””) This formula would return a result of 30°00’00”, which is equivalent to an angle of 0.5236 radians in decimal degrees.
3. Convert angle in degrees, minutes, and seconds to decimal degrees: =DEGREES((30*60+15)*PI()/180/3600) This formula would return a result of 0.50417, which is equivalent to an angle of 30°15’00” in degrees, minutes, and seconds.
4. Convert coordinates from radians to degrees: =DEGREES(ATAN2(5,8)) This formula would return a result of 32.4712 degrees based on the coordinates (5,8).
5. Convert GPS coordinates from decimal degrees to degrees, minutes, and seconds: =TEXT(INT(A2)&”°”&INT((A2-INT(A2))*60)&”‘”&ROUND((((A2-INT(A2))*60)-INT((A2-INT(A2))*60))*60,2)&””””,”0.0000″) This formula would convert a GPS coordinate in decimal degrees to degrees, minutes, and seconds format.
6. Calculate the angle between two points using Cartesian coordinates: =DEGREES(ATAN2(Y2-Y1,X2-X1)) This formula would calculate the angle between two points with Cartesian coordinates (X1,Y1) and (X2,Y2).
7. Convert slope from radians to degrees: =DEGREES(ATAN(0.5)) This formula would convert a slope of 0.5 radians to degrees.
8. Calculate the angle of a right triangle: =DEGREES(ATAN(4/3)) This formula would calculate the angle of a right triangle with sides of length 4 and 3, using the inverse tangent function.
9. Convert an angle in gradians to degrees: =DEGREES(2*PI()*0.9/400) This formula would convert an angle of 0.9 gradians to degrees.
10. Convert an angle in mils to degrees: =DEGREES(1000/64002PI()) This formula would convert an angle of 1000 mils to degrees.

Example 1:

How to use DEGREES function in excel

You can see examples of DEGREES function below:

degrees(A2) ----->>>>answer is  0

degrees(A3) ----->>>>answer is  45

degrees(A4) ----->>>>answer is  60

degrees(A5) ----->>>>answer is  90

degrees(A6) ----->>>>answer is  180

Excel’s DEGREES Function: The Ultimate Guide to Converting Radians to Degrees!

Excel’s DEGREES function is a built-in mathematical function that converts angles in radians to degrees. To use the DEGREES function, simply enter “=DEGREES(angle)” where “angle” is the angle in radians that you want to convert to degrees.

For example, if you have an angle of 2.35619 radians and you want to convert it to degrees, you can use the following formula: =DEGREES(2.35619) This would return a result of approximately 135 degrees.

Mastering the DEGREES Function in Excel: Tips and Tricks You Need to Know

To master the DEGREES function in Excel, consider these tips and tricks:

• Use cell references instead of hardcoding values for ease of modification
• Combine the DEGREES function with other functions such as SIN, COS, or TAN to solve more complex problems
• Use formatting options to display the output in the desired format
• Consider alternative functions such as the RADIANS function for converting angles in degrees to radians

For example, if you have an angle in radians and you want to calculate the sine of that angle in degrees, you can use the following formula: =SIN(DEGREES(A1)) where A1 contains the angle in radians. This would return the sine of the angle in degrees.

Alternatives to the DEGREES Function in Excel: Which One Should You Use?

Excel offers several alternative functions that can be used for converting angles between radians and degrees, including the RADIANS function, which converts angles in degrees to radians, and the TRIGONOMETRIC functions such as SIN, COS, and TAN, which accept inputs in either degrees or radians.

For example, if you have an angle of 45 degrees and you want to convert it to radians, you can use the following formula: =RADIANS(45) This would return a result of approximately 0.7854 radians.

DEGREES Function in Excel: Applying It to Real-World Scenarios

The DEGREES function can be applied to many real-world scenarios such as:

• Calculating angles for navigation and mapping applications
• Converting temperature readings from Celsius to Fahrenheit or vice versa
• Solving trigonometric problems in physics and engineering
• Analyzing data in astronomy, geology, and biology

For example, if you have a temperature reading of 20 degrees Celsius and you want to convert it to Fahrenheit, you can use the following formula: =DEGREES(20*9/5+32) This would return a result of approximately 68 degrees Fahrenheit.

News Alert: Excel’s DEGREES Function Gets Major Update for Improved Accuracy

In a recent update to Excel, Microsoft improved the accuracy of the DEGREES function to handle values up to approximately 1E+308. This update ensures that the DEGREES function returns more accurate results when dealing with very large or very small angles.

For example, if you have an angle of 1E-100 radians and you want to convert it to degrees, you can use the following formula: =DEGREES(1E-100) This would return a result of approximately 5.72958E-98 degrees with improved accuracy.

How to Convert GPS Coordinates Using Excel’s DEGREES Function: A Step-by-Step Guide

To convert GPS coordinates from decimal degrees to degrees, minutes, and seconds format using the DEGREES function in Excel, follow these steps:

1. Enter the decimal degree value into a cell, for example, A1.
2. In another cell, enter the following formula: =TEXT(INT(A1)&”°”&INT((A1-INT(A1))*60)&”‘”&ROUND((((A1-INT(A1))*60)-INT((A1-INT(A1))*60))*60,2)&””””,”0.0000″) This formula converts the decimal degree value in cell A1 to degrees, minutes, and seconds format.
3. Format the output cell as desired.

For example, if you have a GPS coordinate of -33.8568 degrees latitude and you want to convert it to degrees, minutes, and seconds format, you can use the above formula. The output would be “-33°51’24.48″””.

Excel’s DEGREES Function vs. Other Built-In Math Functions – Which One is Right for You?

Excel offers several built-in math functions for converting angles between radians and degrees, including DEGREES, RADIANS, SIN, COS, and TAN. The choice of which function to use depends on the specific needs of the user.

The DEGREES function is used to convert angles in radians to degrees, while the RADIANS function converts angles in degrees to radians. The TRIGONOMETRIC functions (SIN, COS, and TAN) can accept inputs in either radians or degrees.

For example, if you have an angle in degrees and you want to calculate its cosine, you can use the following formula: =COS(RADIANS(A1)) where A1 contains the angle in degrees. This would return the cosine of the angle in radians.

Breaking News: Scientists Use Excel’s DEGREES Function to Solve Complex Calculations

Scientists have recently used Excel’s DEGREES function to solve complex calculations in fields such as physics, engineering, and astronomy. The DEGREES function is a versatile tool for converting angles from radians to degrees, allowing scientists to work with data in a format that is more intuitive and easy to understand.

For example, if a scientist is working with astronomical data that is recorded in radians, they can use the DEGREES function to convert the angle measurements to degrees. This would make it easier to compare and analyze the data, leading to new insights and discoveries.

Beginners’ Guide to Using the DEGREES Function in Excel: Everything You Need to Know

If you’re new to using the DEGREES function in Excel, here are some basic things you should know:

• The DEGREES function is used to convert angles in radians to degrees.
• To use the DEGREES function, enter “=DEGREES(angle)” where “angle” is the angle in radians that you want to convert to degrees.
• You can format the output of the DEGREES function using the Format Cells dialog box.
• The DEGREES function can be used in conjunction with other functions in Excel to perform more complex calculations.

For example, if you have an angle in radians and you want to convert it to degrees, you can use the following formula: =DEGREES(2.35619) This would return a result of approximately 135 degrees.

Latest Research Shows: Excel’s DEGREES Function Boosts Efficiency and Productivity in Math Applications

Recent research has shown that using Excel’s DEGREES function can lead to increased efficiency and productivity in math applications. By converting angles from radians to degrees, users can work with data in a format that is more intuitive and easy to understand, leading to faster and more accurate calculations.

For example, if a user needs to perform multiple calculations involving angles in radians, using the DEGREES function to convert those angles to degrees can save time and reduce errors.

A Comprehensive Look at Excel’s DEGREES Function and Its Role in Solving Trigonometric Problems

Excel’s DEGREES function plays a crucial role in solving trigonometric problems and performing other mathematical calculations. By converting angles from radians to degrees, users can work with data in a format that is more familiar and easier to manipulate.

For example, if a user needs to calculate the hypotenuse of a triangle given its two short sides and an angle in degrees, they can use the following formula: =SQRT(A1^2+B1^2-2A1B1*COS(RADIANS(C1))) where A1 and B1 are the lengths of the two short sides, and C1 is the angle in degrees. This formula uses the COS function with the RADIANS function to convert the angle from degrees to radians.

New Study Finds: Businesses Can Benefit from Excel’s DEGREES Function for Planning and Optimization

A recent study has shown that businesses can benefit from using Excel’s DEGREES function for planning and optimization. By converting angles from radians to degrees, businesses can more easily visualize and analyze data related to location, direction, and orientation.

Excel’s DEGREES Function: Common Errors and How to Avoid Them

Some common errors that can occur when using Excel’s DEGREES function include:

• Using the wrong formula syntax
• Forgetting to convert angles from degrees to radians before using a trigonometric function
• Forgetting to format the output of the DEGREES function
• Using non-numeric values as input for the DEGREES function

To avoid these errors, be sure to double-check your formulas and inputs, use the appropriate conversion functions when necessary, and format your output as desired.

For example, if you have an angle in degrees and you need to calculate its tangent, you can use the following formula: =TAN(RADIANS(A1)) where A1 contains the angle in degrees. This would return the tangent of the angle in radians.

Excel for Mac Users Rejoice: The DEGREES Function is Here to Stay!

Excel users on Mac can rejoice knowing that the DEGREES function is here to stay. Despite some concerns over compatibility issues with the new M1 chip, Microsoft has confirmed that the DEGREES function will continue to be available on all versions of Excel for Mac.

For example, Mac users who need to convert angles from radians to degrees can still rely on the DEGREES function to get the job done.

Why Excel’s DEGREES Function is an Essential Tool for Students, Researchers, and Professionals

Excel’s DEGREES function is an essential tool for students, researchers, and professionals alike because it allows them to work with angles in a format that is more intuitive and easier to understand. By converting angles from radians to degrees, users can perform calculations and analyze data in a way that makes sense to them.

For example, if a student needs to solve a trigonometry problem involving angles in degrees, they can use the DEGREES function to convert those angles to radians and apply the appropriate trigonometric functions. This would make it easier for them to understand and solve the problem.

From Theory to Practice: Using Excel’s DEGREES Function to Solve Real-Life Problems

Excel’s DEGREES function can be used to solve a wide range of real-life problems, from calculating angles for navigation and mapping applications to analyzing data in astronomy, geology, and biology.

For example, if a biologist needs to calculate the angle between two vectors in three-dimensional space, they can use the following formula: =DEGREES(ACOS((A1B1+C1D1+E1*F1)/(SQRT(A1^2+B1^2+C1^2)*SQRT(D1^2+E1^2+F1^2)))) where A1, B1, and C1 represent the x, y, and z components of the first vector, and D1, E1, and F1 represent the x, y, and z components of the second vector. This formula uses the ACOS function with the DEGREES function to convert the output from radians to degrees.

Experts Weigh In: The Pros and Cons of Using Excel’s DEGREES Function vs. Other Software Tools

When it comes to converting angles between radians and degrees, Excel’s DEGREES function is just one of many tools available to users. Some other popular software tools for this task include MATLAB, Python, and Wolfram Mathematica.

The choice of which tool to use depends on factors such as the user’s familiarity with the tool, the specific needs of the project, and the availability of resources. While some users may prefer the simplicity and accessibility of Excel’s DEGREES function, others may require more advanced features and capabilities offered by other tools.

For example, if a user is working on a complex mathematical modeling project that requires high-level programming and advanced data visualization, they may choose to use MATLAB or Python instead of Excel.

Excel’s DEGREES Function Goes Global: How It Supports Internationalization and Localization Efforts

Excel’s DEGREES function is designed to support internationalization and localization efforts by allowing users to work with angles in a variety of units and formats. This can be especially useful for users who need to analyze data from different parts of the world or communicate their findings to an international audience.

For example, if a user needs to convert angles from degrees to radians in order to work with GPS coordinates from around the world, they can use the DEGREES function to do so in a way that is consistent and easily understood.

How to Format the Output of Excel’s DEGREES Function: A Comprehensive Guide

To format the output of Excel’s DEGREES function, follow these steps:

1. Select the cell containing the formula.
2. Right-click and select “Format Cells” from the context menu.
3. In the Format Cells dialog box, select the “Number” tab.
4. Under “Category,” select “Custom.”
5. In the “Type” field, enter the desired format code.

For example, if you want to display the output of the DEGREES function with four decimal places, you can use the following format code: 0.0000

Excel’s DEGREES Function in Action: Case Studies from Different Industries and Disciplines

Excel’s DEGREES function is used in a wide range of industries and disciplines, from engineering and physics to finance and marketing. Here are some examples of how it is used:

• In geology, the DEGREES function is used to convert angles from degrees to radians when calculating distances between two points on a spherical surface.
• In astronomy, the DEGREES function is used to convert celestial coordinates from radians to degrees for easier visualization and analysis.
• In finance, the DEGREES function is used to calculate option prices based on volatility inputs measured in degrees per year.
• In marketing, the DEGREES function is used to map customer locations and calculate sales territories based on geographic boundaries.

For example, a marketing analyst who needs to optimize the distribution of a product across different regions can use the DEGREES function to analyze customer locations and determine the most efficient sales territories based on geographic distance and other factors.

• RADIANS function
• PI function
• SIN function
• COS function
• TRIG function