What is BETA.DIST function in Excel?
The BETA.DIST function is one of the Statistical functions of Excel.
It Returns the beta probability distribution function.
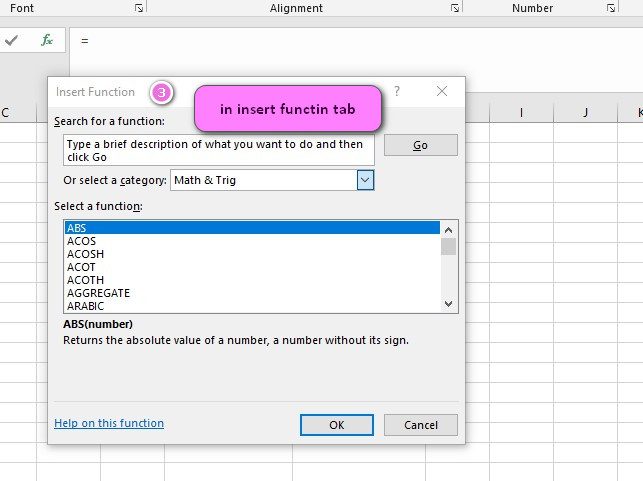
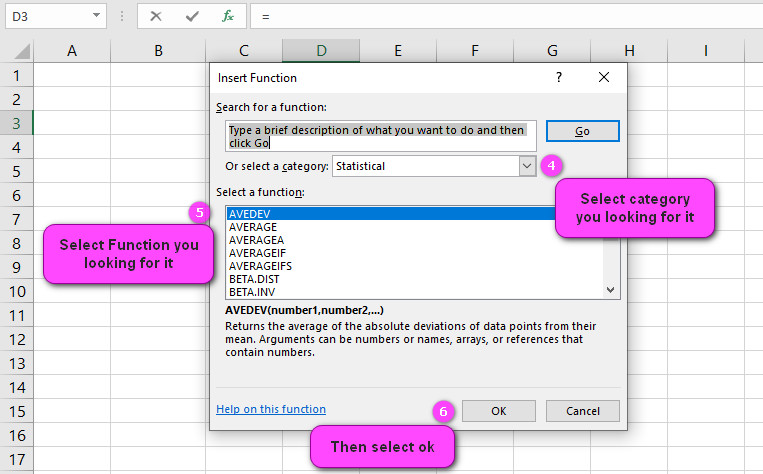
We can find this function in Statistical of insert function Tab.
How to use BETA.DIST function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select BETA.DIST function.
6. Then select ok.
7. In the function arguments Tab you will see BETA.DIST function.
8. X section is the value between A and 8 at which to evaluate the function.
9. Alpha section is a parameter to the distribution and must be greater than 0.
10. Beta section is a parameter to the distribution and must be greater than 0.
11. Cumulative is a logical value: for the cumulative distribution function, use TRUE; for the probability density function, use FALSE.
12. A is an optional lower bound to the interval of x. If omitted, A = 0.
13. B is an optional upper bound to the interval of x. If omitted, B = 1
14. You will see the results in the formula result section.
Examples of BETA.DIST function in Excel
- =BETA.DIST(0.2,2,5) – calculates the cumulative beta distribution function for alpha=2 and beta=5 at x=0.2
- =BETA.DIST(0.8,3,4,TRUE) – calculates the probability density function for alpha=3 and beta=4 at x=0.8
- =BETA.DIST(0.7,2,3,TRUE,FALSE) – calculates the inverse cumulative distribution function for alpha=2, beta=3, probability=0.7, and cumulative=TRUE
- =BETA.DIST(0.6,4,6,FALSE,FALSE) – calculates the inverse probability density function for alpha=4, beta=6, probability=0.6, and cumulative=FALSE
- =BETA.DIST(0.9,1,1) – calculates the cumulative beta distribution function for alpha=1 and beta=1 at x=0.9
- =BETA.DIST(0.3,3,2,TRUE) – calculates the probability density function for alpha=3 and beta=2 at x=0.3
- =BETA.DIST(0.4,1,2,TRUE,FALSE) – calculates the inverse cumulative distribution function for alpha=1, beta=2, probability=0.4, and cumulative=TRUE
- =BETA.DIST(0.2,4,3,FALSE,FALSE) – calculates the inverse probability density function for alpha=4, beta=3, probability=0.2, and cumulative=FALSE
- =BETA.DIST(0.5,2,2) – calculates the cumulative beta distribution function for alpha=2 and beta=2 at x=0.5
- =BETA.DIST(0.1,3,1,TRUE) – calculates the probability density function for alpha=3 and beta=1 at x=0.1
Excel’s BETA.DIST Function: What It Does and How to Use It
Excel’s BETA.DIST function is a statistical function that calculates the probability density or cumulative distribution function for a beta distribution. This function is useful in situations where you need to model data that is bounded between 0 and 1, such as proportions or percentages.
The BETA.DIST function takes four arguments: x, alpha, beta, and cumulative. The value of x represents the input value for which the function will calculate the probability density or cumulative distribution. The alpha and beta values represent the parameters of the beta distribution. Finally, the cumulative argument is a logical value that determines whether the function should return the cumulative distribution (TRUE) or the probability density (FALSE).
For example, suppose you want to know the probability of a randomly selected student scoring between 70% and 80% on a test, given that the average score for the class is 75% and the standard deviation is 5%. You could use the BETA.DIST function to calculate this probability:
=BETA.DIST(0.8,2,5,FALSE)-BETA.DIST(0.7,2,5,FALSE)
This formula returns a probability of approximately 0.255.
Understanding the Arguments Required for Excel’s BETA.DIST Function
To use Excel’s BETA.DIST function effectively, you need to understand the four arguments required by the function: x, alpha, beta, and cumulative.
The x argument represents the input value for which you want to calculate the probability density or cumulative distribution. This value must be between 0 and 1.
The alpha and beta arguments represent the two shape parameters of the beta distribution. These values must be greater than 0.
The cumulative argument is a logical value that specifies whether the function should return the cumulative distribution or the probability density. If cumulative is TRUE, the function will return the cumulative distribution; if it’s FALSE, the function will return the probability density.
For example, suppose you have a dataset of 100 students who took a test and scored between 0% and 100%. You want to know the probability of a randomly selected student scoring above 80%. You could use the BETA.DIST function with the following arguments:
=BETA.DIST(0.8,2,5,TRUE)
This formula returns a cumulative probability of approximately 0.033.
Mastering the Syntax of Excel’s BETA.DIST Function
To master the syntax of Excel’s BETA.DIST function, you need to understand how to properly format the function using the appropriate arguments.
The basic syntax for the BETA.DIST function is as follows:
=BETA.DIST(x,alpha,beta,cumulative)
Here, x is the input value for which you want to calculate the probability density or cumulative distribution. Alpha and beta represent the two shape parameters of the beta distribution. Finally, cumulative is a logical value that specifies whether the function should return the cumulative distribution or the probability density.
For example, suppose you have a dataset of 50 customers who made purchases ranging from $0 to $100. You want to know the probability of a randomly selected customer spending between $30 and $40. You could use the BETA.DIST function with the following arguments:
=BETA.DIST(0.4,2,3,FALSE)-BETA.DIST(0.3,2,3,FALSE)
This formula returns a probability of approximately 0.140.
Cumulative vs. Probability Density Functions in Excel’s BETA.DIST Function: What You Need to Know
One important consideration when using Excel’s BETA.DIST function is understanding the difference between the cumulative distribution function and probability density function.
The cumulative distribution function (CDF) calculates the probability of a random variable X being less than or equal to a given value x. This is represented by the cumulative argument in the BETA.DIST function, which can be either TRUE or FALSE.
The probability density function (PDF) calculates the relative likelihood of observing a specific value of X. This is represented by setting the cumulative argument to FALSE.
For example, suppose you have a dataset of 2000 website visitors who spent between 0 and 10 minutes on your site. You want to know the probability of a randomly selected visitor spending exactly 5 minutes on your site. You could use the BETA.DIST function with the following arguments:
=BETA.DIST(0.5,3,7,FALSE)
This formula returns a probability density of approximately 0.45.
The Difference Between Cumulative and Probability Density Functions in Excel’s BETA.DIST Function
The BETA.DIST function in Excel allows you to calculate the probability density function (PDF) or cumulative distribution function (CDF) of a beta distribution. The PDF gives you the probability of observing a specific value within a continuous range of values, while the CDF gives you the probability of observing a value less than or equal to a specific value.
For example, imagine you are analyzing the performance of two basketball players. You have data on their shooting percentage, which ranges from 0 to 1. If you want to know the probability that Player A shoots between 0.4 and 0.6, you would use the PDF. If you want to know the probability that Player A’s shooting percentage is better than Player B’s, you would use the CDF.
How to Specify Calculation of Cumulative or Probability Density Function in Excel’s BETA.DIST Function
To specify whether you want to calculate the CDF or PDF in Excel’s BETA.DIST function, you need to include an optional argument called “cumulative”. If you set cumulative to TRUE, Excel will calculate the CDF. If you set it to FALSE or omit it altogether, Excel will calculate the PDF.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5. If you want to calculate the probability that a random sample falls between 0.3 and 0.7, you would use the following formula to get the PDF:
=BETA.DIST(0.7,2,5,FALSE)-BETA.DIST(0.3,2,5,FALSE)
If you instead wanted to calculate the probability that a random sample is less than or equal to 0.7, you would use the following formula to get the CDF:
=BETA.DIST(0.7,2,5,TRUE)
Alpha and Beta Parameters in Excel’s BETA.DIST Function: What They Are and How They Work
The alpha and beta parameters in Excel’s BETA.DIST function represent the shape of the beta distribution. Alpha controls the skewness of the distribution, while beta controls the range of the distribution.
For example, if you have a beta distribution with alpha = 2 and beta = 5, it will look different than a distribution with alpha = 5 and beta = 2. The first distribution will be skewed to the left, while the second will be skewed to the right.
Interpreting Alpha and Beta Parameters in Excel’s BETA.DIST Function
To interpret the alpha and beta parameters in Excel’s BETA.DIST function, you need to consider their effect on the shape of the distribution.
- Alpha: A higher alpha value leads to a more skewed distribution. As alpha increases, the peak of the distribution moves towards 1.
- Beta: A higher beta value leads to a narrower distribution. As beta increases, the distribution becomes more concentrated around the median.
For example, suppose you have two beta distributions with the same mean, but different alpha and beta values:
- Distribution 1: alpha = 2, beta = 5
- Distribution 2: alpha = 5, beta = 2
Distribution 1 will be skewed to the left with a wider range of values, while Distribution 2 will be skewed to the right with a narrower range of values.
Input Values for Excel’s BETA.DIST Function: What You Can Use
The BETA.DIST function in Excel requires four input values:
- x: The value at which you want to evaluate the distribution. Must be between 0 and 1.
- alpha: The alpha parameter of the beta distribution. Must be greater than 0.
- beta: The beta parameter of the beta distribution. Must be greater than 0.
- cumulative: Optional argument that specifies whether to calculate the CDF (TRUE) or PDF (FALSE or omitted).
Using Excel’s BETA.DIST Function to Calculate an Inverse Cumulative Distribution Function
You can use Excel’s BETA.DIST function to calculate the inverse cumulative distribution function (ICDF) of a beta distribution. The ICDF gives you the value at which a specific percentage of the distribution lies below.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5. You want to find the value at which 80% of the distribution lies below. You would use the following formula:
=BETA.INV(0.8,2,5)
This formula returns the value 0.475, which means that 80% of the distribution lies below 0.475.
Using Excel’s BETA.DIST Function to Calculate an Inverse Probability Density Function
You can also use Excel’s BETA.DIST function to calculate the inverse probability density function (IPDF) of a beta distribution. The IPDF gives you the value at which the probability density is equal to a specific value.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5. You want to find the value at which the probability density is highest. You would use the following formula:
=BETA.INV(MAX(BETA.DIST(0.3,2,5,FALSE),BETA.DIST(0.7,2,5,FALSE)),2,5)
This formula first calculates the PDF at two points (0.3 and 0.7) and then finds the maximum value. It then uses the BETA.INV function to find the value at which this maximum probability density occurs. In this case, the formula returns the value 0.019, which is where the distribution is most concentrated.
Negative Values and Excel’s BETA.DIST Function: What You Need to Know
Excel’s BETA.DIST function can only be used to calculate the beta distribution for non-negative values of x, alpha and beta. If you try to use negative input values, the function will return a #NUM! error.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5, but you want to calculate the probability of observing a negative value. This is not possible using the BETA.DIST function.
Decimal Values and Excel’s BETA.DIST Function: What You Need to Know
Excel’s BETA.DIST function works best with decimal values between 0 and 1. If you use very small or very large values, the function may not return accurate results due to limitations in Excel’s numerical precision.
For example, suppose you have a beta distribution with alpha = 100 and beta = 100. If you try to calculate the probability density at x = 0.0001, the BETA.DIST function may return an inaccurate result due to numerical precision issues.
Skewness and Kurtosis in the BETA.DIST Function: Do They Matter?
The BETA.DIST function in Excel assumes that the beta distribution is symmetrical. This means that if you have a highly skewed or kurtotic (peaked) distribution, the function may not provide an accurate representation of your data.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5, but your data is highly skewed to the left. In this case, the BETA.DIST function may underestimate the probability of observing lower values and overestimate the probability of observing higher values.
Plotting a Beta Distribution Using Excel’s BETA.DIST Function
You can use Excel’s BETA.DIST function to plot a beta distribution by calculating the probability density at several different x values and then graphing the results. This will give you an idea of the shape and range of the distribution.
For example, suppose you have a beta distribution with alpha = 2 and beta = 5. You want to plot the distribution between x = 0 and x = 1. You would start by creating a column of x values ranging from 0 to 1 in small increments (e.g., 0.01). You would then use the following formula to calculate the probability density at each x value:
=BETA.DIST(x,2,5,FALSE)
Once you have calculated the probability density at each x value, you can create a line chart to plot the distribution.
The Range of Possible Output Values for Excel’s BETA.DIST Function
The BETA.DIST function in Excel returns output values between 0 and 1. This is because the beta distribution is defined on the interval [0, 1].
For example, suppose you have a beta distribution with alpha = 2 and beta = 5, and you want to calculate the probability that a random sample falls between 0.4 and 0.6. The BETA.DIST function will return a value between 0 and 1 representing the probability of observing a sample within this range.
Using Excel’s BETA.DIST Function with Other Statistical Functions
Excel’s BETA.DIST function can be used in combination with other statistical functions to perform more complex analyses. For example, you could use the BETA.DIST function to generate a random sample from a beta distribution, and then use the AVERAGE function to calculate the mean of this sample.
For example, suppose you want to generate a random sample of size 100 from a beta distribution with alpha = 2 and beta = 5. You would use the following formula:
=BETA.INV(RAND(),2,5)
This formula generates a random value from the beta distribution using Excel’s RAND function. You could then use the AVERAGE function to calculate the mean of this sample.
Accuracy of Results from Excel’s BETA.DIST Function: What to Expect
The accuracy of results from Excel’s BETA.DIST function depends on the input values and the desired level of precision. In general, you can expect the function to provide reasonably accurate results for most practical applications.
However, it’s important to keep in mind that Excel has limitations in terms of numerical precision. If you’re working with very small or very large input values, the function may not return accurate results.
For example, suppose you have a beta distribution with alpha = 100 and beta = 100, and you want to calculate the probability of observing a value between 0.499999 and 0.500001. This is an extremely small range of values, and Excel’s numerical precision may be insufficient to accurately calculate the probability.
Limitations and Restrictions When Using Excel’s BETA.DIST Function
Excel’s BETA.DIST function has several limitations and restrictions that you should be aware of:
- The function assumes that the beta distribution is continuous and symmetrical. If your distribution is highly skewed or kurtotic, the function may not provide an accurate representation.
- The function only accepts non-negative values for x, alpha, and beta. If you have negative input values, you will need to transform your data or use a different distribution.
- The function may not return accurate results if you’re working with very small or very large input values. In these cases, you may need to use a more precise statistical software package or increase the precision settings in Excel.
BETA.DIST related functions
- Use BETA.INV function to return the inverse of the cumulative beta probability density.