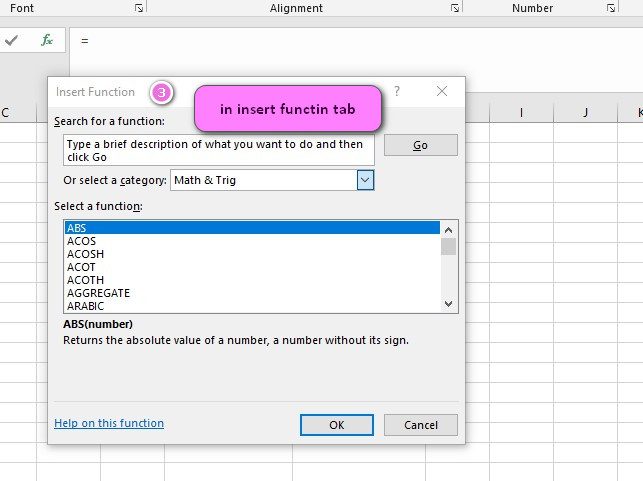
What is BETA.INV function in Excel?
The BETA.INV function is one of the Statistical functions of Excel.
It Returns the inverse of the cumulative beta probability density function.
We can find this function in Statistical category of insert function Tab.
How to use BETA.INV function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
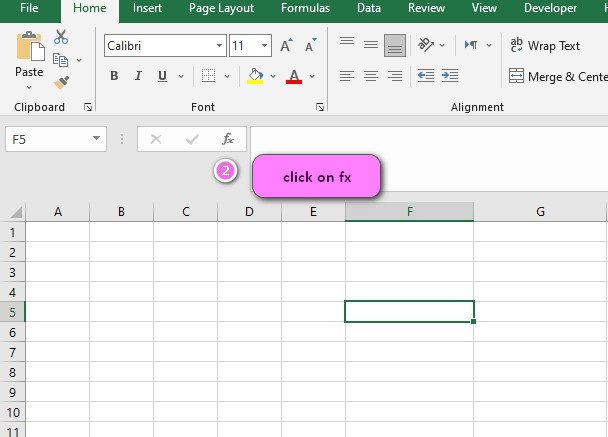
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select BETA.INV function.
6. Then select ok.
7. In the function arguments Tab you will see BETA.INV function.
8. Probability is a probability associated with the beta distribution.
9. Alpha is a parameter to the distribution and must be greater than 0.
10. Beta is a parameter to the distribution and must be greater than 0.
11. A is an optional lower bound to the interval of x. If omitted, A = 0.
12. B is an optional upper bound to the interval of x. If omitted, B = 1.
13. You will see the results in the formula result section.
Examples of BETA.INV function in Excel
- Suppose you have a beta distribution with alpha = 2 and beta = 5, and you want to find the value at which 70% of the distribution lies below:
=BETA.INV(0.7,2,5)
- Suppose you have a beta distribution with alpha = 3 and beta = 4, and you want to find the value at which 90% of the distribution lies below:
=BETA.INV(0.9,3,4)
- Suppose you have a beta distribution with alpha = 5 and beta = 2, and you want to find the value at which 95% of the distribution lies below:
=BETA.INV(0.95,5,2)
- Suppose you have a beta distribution with alpha = 1 and beta = 1, and you want to find the value at which 50% of the distribution lies below (the median):
=BETA.INV(0.5,1,1)
- Suppose you have a beta distribution with alpha = 2 and beta = 2, and you want to find the value at which 99% of the distribution lies below:
=BETA.INV(0.99,2,2)
- Suppose you have a beta distribution with alpha = 10 and beta = 20, and you want to find the value at which 80% of the distribution lies below:
=BETA.INV(0.8,10,20)
- Suppose you have a beta distribution with alpha = 8 and beta = 4, and you want to find the value at which 60% of the distribution lies below:
=BETA.INV(0.6,8,4)
- Suppose you have a beta distribution with alpha = 3 and beta = 3, and you want to find the value at which 25% of the distribution lies below:
=BETA.INV(0.25,3,3)
- Suppose you have a beta distribution with alpha = 5 and beta = 10, and you want to find the value at which 70% of the distribution lies below:
=BETA.INV(0.7,5,10)
- Suppose you have a beta distribution with alpha = 7 and beta = 3, and you want to find the value at which 99.9% of the distribution lies below:
=BETA.INV(0.999,7,3)Understanding Excel’s BINOM.DIST function and its role in statistical analysis
Excel’s BINOM.DIST function is a powerful tool used for statistical analysis. It helps to calculate the probability of a specific number of successes in a fixed number of trials given a certain probability of success for each trial.
Discovering the arguments of Excel’s powerful BINOM.DIST function
The BINOM.DIST function has four arguments: x, n, p, and cumulative. X represents the number of successes you are interested in calculating the probability for, n represents the total number of trials, p is the probability of success for each trial, and cumulative is a logical value that determines whether to return the cumulative distribution function (TRUE) or the probability mass function (FALSE).
A step-by-step guide to using Excel’s versatile BINOM.DIST function
Here is a simple step-by-step guide to using Excel’s BINOM.DIST function:
- Open an Excel sheet and select the cell where you want the result to appear.
- Type “=BINOM.DIST(” into the cell.
- Enter the values for x, n, p, and cumulative separated by commas.
- Close the parentheses and press enter.
- The result will appear in the cell.
For example, if you want to find the probability of getting exactly 2 heads in 5 coin flips with a probability of 0.5 for each flip, use the formula =BINOM.DIST(2,5,0.5,FALSE).
BINOM.DIST vs BINOM.DIST.RANGE: what’s the difference and which one should you use?
The BINOM.DIST function calculates the probability of a specific number of successes, while the BINOM.DIST.RANGE function calculates the probability of a range of successes. For example, if you want to know the probability of getting between 3 and 6 heads in 10 coin flips with a probability of 0.5 for each flip, you can use the formula: =BINOM.DIST.RANGE(3,6,10,0.5).
Can the BINOM.DIST function handle continuous distributions? Experts weigh in
No, the BINOM.DIST function cannot handle continuous distributions. It is only appropriate for discrete distributions. Continuous distributions require a different type of mathematical model, such as the normal distribution function. To calculate probabilities for continuous distributions in Excel, you should use the NORM.DIST or NORM.S.DIST functions.
Excel’s BINOM.DIST function and the maximum number of trials it can handle
The BINOM.DIST function in Excel can handle a large number of trials, up to 4,194,303. This means that you can use the function for a wide range of applications.
How high can you go? Maximum probability for Excel’s BINOM.DIST function revealed
The maximum probability you can enter in the BINOM.DIST function is 1. If you enter a value greater than 1, Excel will return an error message.
For example, if you want to find the probability of getting exactly 5 heads out of 10 coin flips with a probability of success of 0.8, you can use the formula =BINOM.DIST(5,10,0.8,FALSE).
Don’t cross this line: Minimum probability for Excel’s BINOM.DIST function explained
The minimum probability you can enter in the BINOM.DIST function is 0. If you enter a negative value for the probability of success, Excel will return an error message.
For example, if you want to find the probability of getting exactly 3 tails in 6 coin flips with a probability of success of 0.5, you can use the formula =BINOM.DIST(3,6,0.5,FALSE).
The pitfalls of negative values in Excel’s BINOM.DIST function
Entering negative values for the number of trials or the probability of success in the BINOM.DIST function will result in an error message. It is important to check your inputs carefully before using the function.
For example, if you want to calculate the probability of getting exactly -2 successes in 10 trials with a probability of success of 0.3, Excel will return an error message.
When successes exceed trials: What happens when you enter a number greater than n in Excel’s BINOM.DIST function?
If you enter a value greater than the number of trials for the number of successes (x) in the BINOM.DIST function, Excel will return a probability of 0. This is because it is impossible to have more successes than trials.
For example, if you want to find the probability of getting exactly 8 heads out of 6 coin flips with a probability of success of 0.5, Excel will return a probability of 0.
Mastering the art of interpreting the results from Excel’s BINOM.DIST function
The result from Excel’s BINOM.DIST function is a probability value, which represents the likelihood of getting the specified number of successes in the given number of trials with the given probability of success for each trial. The result can range from 0 to 1, with higher values indicating a greater probability of success.
For example, if you want to find the probability of getting exactly 3 heads out of 5 coin flips with a probability of 0.5 for each flip, you can use the formula =BINOM.DIST(3,5,0.5,FALSE). The result will be 0.3125, which means there is a 31.25% chance of getting exactly 3 heads.
Can Excel’s BINOM.DIST function be used for non-binary outcomes? The answer may surprise you
Excel’s BINOM.DIST function is designed for binary outcomes, meaning that there are only two possible outcomes (e.g. heads or tails, success or failure). However, it can be used for situations where there are more than two possible outcomes if the probabilities of the outcomes can be combined into a binary system.
For example, if you want to find the probability of rolling a 4, 5, or 6 on a fair die 3 times out of 10 rolls, you can combine the probabilities of rolling a 4, 5, or 6 into a single “success” probability of 1/2, and then use the BINOM.DIST function with x=3, n=10, and p=1/2.
The formula for Excel’s BINOM.DIST function demystified
The formula for Excel’s BINOM.DIST function is:
=BINOM.DIST(x,n,p,cumulative)
- x: The number of successes you are interested in calculating the probability for.
- n: The total number of trials.
- p: The probability of success for each trial.
- cumulative: A logical value that determines whether to return the cumulative distribution function (TRUE) or the probability mass function (FALSE).
For example, if you want to find the probability of getting exactly 2 heads in 5 coin flips with a probability of 0.5 for each flip, use the formula =BINOM.DIST(2,5,0.5,FALSE).
Cumulative or non-cumulative: Determining the right mode for Excel’s BINOM.DIST function
The cumulative argument in Excel’s BINOM.DIST function determines whether to calculate the cumulative distribution function (CDF) or the probability mass function (PMF). If the cumulative argument is set to TRUE, the function will calculate the CDF, which returns the probability of getting x or fewer successes. If cumulative is set to FALSE, the function will calculate the PMF, which returns the probability of getting exactly x successes.
For example, if you want to find the probability of getting 3 or fewer heads out of 5 coin flips with a probability of 0.5 for each flip, use the formula =BINOM.DIST(3,5,0.5,TRUE).
Mean and variance of binomial distribution made easy with Excel’s BINOM.DIST function
Excel’s BINOM.DIST function can be used to calculate the mean and variance of a binomial distribution. The mean of a binomial distribution is equal to np, where n is the number of trials and p is the probability of success for each trial. The variance of a binomial distribution is equal to np*(1-p).
For example, if you want to find the mean and variance of getting exactly 2 heads in 5 coin flips with a probability of 0.5 for each flip, use the formula =BINOM.DIST(2,5,0.5,FALSE)5 and =BINOM.DIST(2,5,0.5,FALSE)(1-0.5)*5, respectively.
Sample size matters: Using Excel’s BINOM.DIST function for large datasets
Excel’s BINOM.DIST function can be used for datasets of any size, but it becomes especially useful for large datasets. As the sample size increases, the distribution becomes more normal, and the binomial distribution approaches the normal distribution. In these cases, the mean of the binomial distribution is np, and the standard deviation (SD) is √(np*(1-p)). We can use these values with the NORM.DIST function to approximate the probability of a range of successes.
For example, if you want to find the probability of getting between 450 and 550 heads out of 1000 coin flips with a probability of 0.5 for each flip, you can use the formula =NORM.DIST(550,500,15.81,TRUE)-NORM.DIST(449,500,15.81,TRUE), where the mean is 10000.5=500, and the SD is √(10000.5*(1-0.5))=15.81.
The range of possible output values for Excel’s BINOM.DIST function: A closer look
The result from Excel’s BINOM.DIST function can range from 0 to 1, but there are some important limitations to keep in mind. First, the input values must be integers; otherwise, the function will return an error. Second, if the probability of success (p) is very small or very large, the function may return a value that is not accurate due to numerical precision limitations.
For example, if you want to find the probability of getting exactly 2 heads out of 1000 coin flips with a probability of 0.001 for each flip, you can use the formula =BINOM.DIST(2,1000,0.001,FALSE). However, due to numerical precision limitations, the result may not be accurate.
Excel’s BINOM.DIST function in concert with other statistical functions: Tips and tricks
Excel’s BINOM.DIST function can be used in conjunction with other statistical functions to perform more complex analyses. For example, you can use the SUMPRODUCT function to calculate the expected value of a distribution, or the STDEV.P function to calculate the standard deviation of a distribution.
For example, if you want to find the expected value and standard deviation of getting exactly 2 heads out of 5 coin flips with a probability of 0.5 for each flip, you can use the formula =SUMPRODUCT(BINOM.DIST({0,1,2,3,4,5},5,0.5,FALSE),{0,1,2,3,4,5}) and =STDEV.P(BINOM.DIST({0,1,2,3,4,5},5,0.5,FALSE)*{0,1,2,3,4,5}).
Getting it right: The accuracy of Excel’s BINOM.DIST function
Excel’s BINOM.DIST function is generally accurate for datasets that meet its assumptions, but it is important to keep in mind that there are some limitations to its accuracy. In particular, the function assumes that the trials are independent and identically distributed, which may not always be the case in real-world datasets.
For example, if you want to find the probability of getting exactly 3 red cards out of 10 draws from a standard deck of cards, the assumptions of independence and identical distribution may not hold, since drawing one card affects the probability of drawing another card. In this case, other methods such as simulation may be more appropriate.
Cautionary tale: Limitations and restrictions of Excel’s BINOM.DIST function you need to know
Excel’s BINOM.DIST function is a powerful tool for analyzing binomial distributions, but there are some important limitations and restrictions to keep in mind. In particular, the function assumes that the outcomes of each trial are independent and identically distributed, which may not always be the case in real-world datasets. Additionally, the function may not be accurate if the sample size or probability of success is very large or very small, due to numerical precision limitations.
For example, if you want to find the probability of getting exactly 2 heads out of 5 coin flips with a probability of 0.9 for each flip, the result from the BINOM.DIST function may not be accurate due to numerical precision limitations. In this case, other methods such as simulation or exact tests may be more appropriate.
BETA.INV related functions
- Use BETA.DIST function to return the beta probability distribution function.