What is CHISQ.TEST function in Excel?
The CHISQ.TEST function is one of the Statistical functions of Excel.
It Returns the test for independence: the value from the chi-squared distribution for the statistic and the appropriate degrees of freedom.
We can find this function in Statistical category of the insert function Tab.
How to use CHISQ.TEST function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
3. In the insert function tab you will see all functions.
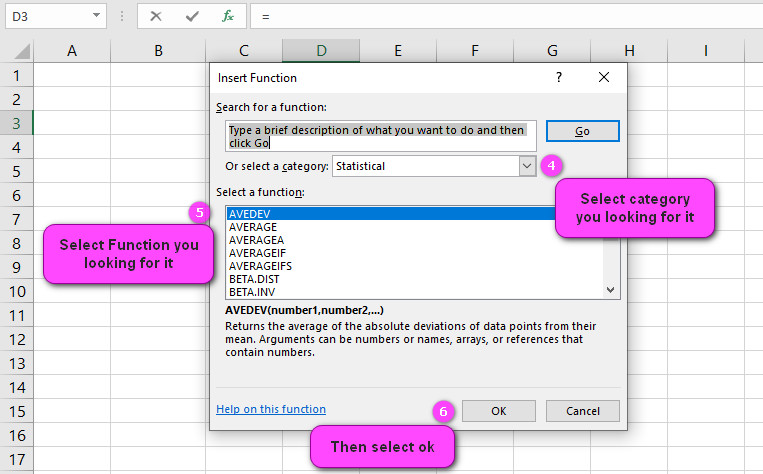
4. Select STATISTICAL category.
5. Select CHISQ.TEST function.
6. Then select ok.
7. In the function arguments Tab you will see CHISQ.TEST function.
8. Actual_range is the range of data that contains observations to test against expected values.
9. Expected_range is the range of data that contains the ratio of the product of row totals and column totals to the grand total.
10. You will see the results in the formula result section.
Examples of CHISQ.TEST function in Excel
- Test whether observed frequencies match expected frequencies for a particular distribution:
=CHISQ.TEST(A1:A6,B1:B6)
Where A1:A6 contains the observed frequencies and B1:B6 contains the expected frequencies.
- Test whether two sets of observed frequencies come from the same population:
=CHISQ.TEST(A1:C2)
Where A1:C2 contains the two sets of observed frequencies.
- Test whether there is a significant difference between the proportion of people who prefer Coke versus Pepsi:
=CHISQ.TEST(A1:A2,B1:B2)
Where A1:A2 contains the number of people who prefer Coke and B1:B2 contains the number of people who prefer Pepsi.
- Test whether there is an association between gender and smoking status:
=CHISQ.TEST(A1:B3)
Where A1:B3 contains a contingency table of gender (rows) and smoking status (columns).
- Test whether a sample of data follows a Poisson distribution with a mean of 5:
=CHISQ.TEST(A1:A5,POISSON.DIST(B1:B5,5,TRUE))
Where A1:A5 contains the observed frequencies and POISSON.DIST(B1:B5,5,TRUE) contains the expected frequencies based on a Poisson distribution with a mean of 5.
- Test whether a sample of data follows a normal distribution with a mean of 100 and a standard deviation of 10:
=CHISQ.TEST(A1:A10,NORM.DIST(B1:B10,100,10,TRUE))
Where A1:A10 contains the observed frequencies and NORM.DIST(B1:B10,100,10,TRUE) contains the expected frequencies based on a normal distribution with a mean of 100 and a standard deviation of 10.
- Test whether there is a significant difference in the proportion of people who prefer red, blue, or green apples:
=CHISQ.TEST(A1:A3,SUM(A1:A3)/SUM(B1:B3)*B1:B3)
Where A1:A3 contains the number of people who prefer red, blue, or green apples and B1:B3 contains the total number of people surveyed.
- Test whether observed frequencies match expected frequencies for a particular distribution with 6 degrees of freedom:
=CHISQ.TEST(A1:A6,B1:B6,6)
Where A1:A6 contains the observed frequencies and B1:B6 contains the expected frequencies, and 6 represents the degrees of freedom.
- Test whether there is a significant difference between the proportion of people who prefer coffee versus tea at different times of day:
=CHISQ.TEST({A1:B3,C1:D3})
Where A1:B3 contains the number of people who prefer coffee or tea in the morning and C1:D3 contains the number of people who prefer coffee or tea in the afternoon.
- Test whether there is a significant difference between observed frequencies and expected frequencies based on a uniform distribution:
=CHISQ.TEST(A1:A5,UNIFORM.DIST(B1:B5,MIN(B1:B5),MAX(B1:B5),TRUE))
Where A1:A5 contains the observed frequencies and UNIFORM.DIST(B1:B5,MIN(B1:B5),MAX(B1:B5),TRUE) contains the expected frequencies based on a uniform distribution with a minimum value of MIN(B1:B5) and a maximum value of MAX(B1:B5).
“Excel’s CHISQ.TEST Function: A Comprehensive Guide”
The CHISQ.TEST function in Excel is used to perform a chi-square goodness-of-fit test, which compares the observed frequencies of data to the expected frequencies. This function is useful for determining whether there is a significant difference between two sets of data or whether a set of data fits a particular distribution.
For example, if we want to test whether a sample of data follows a normal distribution with a mean of 50 and a standard deviation of 10 (null hypothesis) or not (alternative hypothesis), we can use the CHISQ.TEST function in Excel to calculate the chi-square statistic and compare it to the critical value at a certain level of significance based on the degrees of freedom.
“When to Use Excel’s CHISQ.TEST Function for Statistical Analysis”
The CHISQ.TEST function in Excel should be used when comparing observed frequencies of data to expected frequencies, such as in a goodness-of-fit test or a test of independence using a contingency table. This function is commonly used in statistical analysis when working with categorical or discrete data.
For example, if we want to test whether there is a significant association between the type of car a person drives and their income level, we can create a contingency table in Excel and use the CHISQ.TEST function to calculate the chi-square statistic and find the probability of observing the data under the null hypothesis of independence.
“Understanding the Output of Excel’s CHISQ.TEST Function”
The CHISQ.TEST function in Excel returns the probability of observing the data under the null hypothesis of no difference or independence. This probability is commonly referred to as the p-value, and it is used to determine whether to reject or fail to reject the null hypothesis.
For example, if we use the CHISQ.TEST function in Excel to test whether a sample of data follows a Poisson distribution with a mean of 3, and the resulting p-value is 0.05, we can reject the null hypothesis at a significance level of 0.05 and conclude that the data does not follow a Poisson distribution with a mean of 3.
“An Overview of the Arguments in Excel’s CHISQ.TEST Function”
The CHISQ.TEST function in Excel has one required argument and two optional arguments. The required argument is the range of observed frequencies or a single array of data. The first optional argument is the range of expected frequencies or a single array of data, and the second optional argument is the number of degrees of freedom.
For example, if we want to test whether a sample of data follows a uniform distribution, we can use the CHISQ.TEST function in Excel with the following arguments:
=CHISQ.TEST(A1:A10,UNIFORM.DIST(A1,A10,MIN(A1:A10),MAX(A1:A10),TRUE))
Where A1:A10 contains the observed data and UNIFORM.DIST(A1,A10,MIN(A1:A10),MAX(A1:A10),TRUE) contains the expected frequencies based on a uniform distribution with a minimum value of MIN(A1:A10) and a maximum value of MAX(A1:A10).
“Interpreting the Results of Excel’s CHISQ.TEST Function: What Do They Mean?”
The results of the CHISQ.TEST function in Excel are interpreted based on the significance level chosen for the test. If the p-value is less than the significance level (usually 0.05), then the null hypothesis is rejected, and there is evidence of a significant difference between the observed and expected frequencies. If the p-value is greater than or equal to the significance level, then the null hypothesis cannot be rejected, and there is insufficient evidence of a significant difference.
For example, if we use the CHISQ.TEST function in Excel to test whether a sample of data follows a binomial distribution with a probability of success of 0.8, and the resulting p-value is 0.03, we can reject the null hypothesis at a significance level of 0.05 and conclude that the data does not follow a binomial distribution with a probability of success of 0.8.
“Chi-Square Goodness-of-Fit Tests: How to Use Excel’s CHISQ.TEST Function”
A chi-square goodness-of-fit test is used to determine whether a sample of data follows a particular distribution or not. The CHISQ.TEST function in Excel can be used to perform this test by comparing the observed frequencies of the data to the expected frequencies based on the null hypothesis.
For example, if we want to test whether a sample of data follows a normal distribution with a mean of 5 and a standard deviation of 1, we can use the CHISQ.TEST function in Excel with the following arguments:
=CHISQ.TEST(A1:A10,NORM.DIST(A1:A10,5,1,TRUE))
Where A1:A10 contains the observed data and NORM.DIST(A1:A10,5,1,TRUE) contains the expected frequencies based on a normal distribution with a mean of 5 and a standard deviation of 1.
“Contingency Tables and Excel’s CHISQ.TEST Function: An Introduction”
A contingency table is a table that displays the frequency distribution of two categorical variables. The CHISQ.TEST function in Excel can be used to perform a test of independence on a contingency table to determine whether there is a significant association between the two variables.
For example, if we have a contingency table that shows the number of people who prefer Coke or Pepsi based on their gender, we can use the CHISQ.TEST function in Excel to test whether there is a significant association between gender and soda preference.
“Creating Contingency Tables in Excel for Use with CHISQ.TEST Function”
To create a contingency table in Excel, we can use the COUNTIFS function to count the number of observations that fall into each category.
For example, if we have a dataset that includes the age and income level of individuals, we can create a contingency table in Excel that shows the number of individuals in each age group and income level by using the following formula:
=COUNTIFS(A1:A100,"<25",B1:B100,"<50000")
Where A1:A100 contains the age data and B1:B100 contains the income data.
“Calculating Expected Frequencies for a Contingency Table in Excel”
To perform a test of independence on a contingency table using the CHISQ.TEST function in Excel, we must also calculate the expected frequencies based on the null hypothesis of independence. The expected frequencies can be calculated using the row and column totals of the contingency table.
For example, if we have a contingency table that shows the number of people who prefer Coke or Pepsi based on their gender, we can calculate the expected frequencies using the following formula:
=SUM(A2:A3)*SUM(B2:C2)/SUM(B2:C3)
Where A2:A3 contains the row totals and B2:C2 contains the column totals.
“Null Hypothesis Testing with Excel’s CHISQ.TEST Function”
The CHISQ.TEST function in Excel is commonly used to perform null hypothesis testing, which involves testing whether there is a significant difference between two sets of data or whether a set of data follows a particular distribution. The null hypothesis assumes that there is no significant difference or relationship between the variables being tested.
For example, if we want to test whether there is a significant difference between the proportion of people who prefer red, blue, or green apples, we can use the CHISQ.TEST function in Excel with the following arguments:
=CHISQ.TEST(A1:A3,SUM(A1:A3)/SUM(B1:B3)*B1:B3)
Where A1:A3 contains the number of people who prefer red, blue, or green apples and B1:B3 contains the total number of people surveyed. The null hypothesis assumes that there is no significant difference between the proportions of people who prefer each type of apple.
“Alternative Hypotheses and Excel’s CHISQ.TEST Function: A Guide”
An alternative hypothesis is a statement that contradicts the null hypothesis in a statistical test. The CHISQ.TEST function in Excel can be used to test alternative hypotheses by comparing the observed frequencies of data to the expected frequencies based on the alternative hypothesis.
For example, if we want to test whether a sample of data follows a normal distribution with a mean of 5 and a standard deviation of 1 (alternative hypothesis), we can use the CHISQ.TEST function in Excel with the following arguments:
=CHISQ.TEST(A1:A10,NORM.DIST(A1:A10,5,1,FALSE))
Where A1:A10 contains the observed data and NORM.DIST(A1:A10,5,1,FALSE) contains the expected frequencies based on a normal distribution with a mean of 5 and a standard deviation of 1.
“Choosing Significance Levels for Chi-Square Tests Using Excel’s CHISQ.TEST Function”
In a chi-square test, the significance level is the probability of rejecting the null hypothesis when it is actually true. The significance level is typically set at 0.05, but it can be adjusted depending on the specific needs of the analysis.
For example, if we want to test whether there is a significant difference between the number of men and women who prefer coffee or tea, we can use the CHISQ.TEST function in Excel and set the significance level to 0.01 if we want to have a lower likelihood of making a Type I error (rejecting the null hypothesis when it is actually true).
“Degrees of Freedom in Chi-Square Tests: An Explanation for Use with Excel’s CHISQ.TEST Function”
The degrees of freedom (df) in a chi-square test refer to the number of independent variables that are being analyzed. The df can be calculated by subtracting one from the number of categories in each variable and then multiplying the results.
For example, if we are analyzing a contingency table with four rows and three columns, the df would be (4-1) x (3-1) = 6.
“Understanding Degrees of Freedom and Their Importance in Chi-Square Testing with Excel’s CHISQ.TEST Function”
The degrees of freedom in a chi-square test are important because they determine the critical values that are used to interpret the test results. The critical values are determined based on the df and the significance level chosen for the test.
For example, if we use the CHISQ.TEST function in Excel to test whether a sample of data follows a Poisson distribution with a mean of 3, and the resulting df is 5, we can look up the critical value in a chi-square distribution table with 5 degrees of freedom and the chosen significance level to determine whether to reject or fail to reject the null hypothesis.
“P-Values and Excel’s CHISQ.TEST Function: What Are They and How to Interpret Them”
In a chi-square test, the p-value is the probability of observing the data under the null hypothesis of no difference or independence. The p-value is typically compared to the significance level to determine whether to reject or fail to reject the null hypothesis.
For example, if we use the CHISQ.TEST function in Excel to test whether there is a significant association between the type of exercise a person does and their risk of heart disease, and the resulting p-value is 0.02, we can reject the null hypothesis at a significance level of 0.05 and conclude that there is a significant association between exercise type and heart disease risk.
“Interpreting P-Values from Chi-Square Tests Using Excel’s CHISQ.TEST Function”
The p-value in a chi-square test using the CHISQ.TEST function in Excel is a measure of the strength of evidence against the null hypothesis. The p-value tells us the probability of observing the data that we have if the null hypothesis is true.
For example, if we use the CHISQ.TEST function in Excel to test whether there is a significant association between a person’s age group and their cigarette smoking status, and the resulting p-value is 0.001, we can conclude that the chance of observing the data if there is no relationship between age group and smoking status is very low. Therefore, we can reject the null hypothesis at a significance level of 0.05 and conclude that there is a significant association between age group and smoking status.
“Using Excel’s CHISQ.TEST Function with Non-Numeric Data”
The CHISQ.TEST function in Excel can still be used with non-numeric data by converting the categorical or discrete data into numerical values. For example, we can assign a numerical value to each category or create dummy variables to represent the categories.
For example, if we want to test whether there is a significant difference in the number of people who prefer different brands of soda based on their political affiliation (Republican, Democrat, Independent), we can use the CHISQ.TEST function in Excel after converting the political affiliation data into numerical values (e.g., Republican = 1, Democrat = 2, Independent = 3).
“Handling Missing Values in Chi-Square Testing with Excel’s CHISQ.TEST Function”
Missing values can be handled in a chi-square test using the CHISQ.TEST function in Excel by deleting the observations that contain missing data or by imputing the missing values. If the missing values are assumed to be missing completely at random, then imputation can be used to estimate the missing values.
For example, if we have a contingency table that shows the number of people who prefer different types of meat based on their income level, and some of the income data is missing, we can impute the income data using a regression model and then use the CHISQ.TEST function in Excel to test for independence between meat preference and income level.
“Improving the Power of Chi-Square Tests with Excel’s CHISQ.TEST Function”
The power of a chi-square test using the CHISQ.TEST function in Excel can be improved by increasing the sample size or by choosing a more appropriate test statistic. Increasing the sample size can improve the ability of the test to detect small differences, while choosing a more appropriate test statistic can improve the sensitivity of the test to specific types of differences.
For example, if we want to test whether there is a significant difference in the response rates to a new drug treatment between two groups (treatment and control), we can increase the power of the test by increasing the sample size or by using a more appropriate test statistic such as Fisher’s exact test.
“Comparing Two Sets of Data with Excel’s CHISQ.TEST Function: A Guide”
The CHISQ.TEST function in Excel can be used to compare two sets of data by creating a contingency table that shows the frequency distribution of the data for each group. The test can then be performed to determine whether there is a significant difference between the groups.
For example, if we want to test whether there is a significant difference between the proportion of men and women who smoke, we can create a contingency table in Excel that shows the number of smokers and non-smokers for each gender, and then use the CHISQ.TEST function in Excel to test for independence between smoking status and gender.
CHISQ.TEST related functions
- Use CHISQ.DIST function to return the left-tailed probability of the chi-squared distribution.
- Use CHISQ.DIST.RT function to return the right-tailed probability of the chi-squared distribution.
- Use CHISQ.INV function to return the inverse of the left-tailed probability of the chi-squared distribution.
- Use CHISQ.INV.RT function to return the inverse of the right-tailed probability of the chi-squared distribution.