What is CONFIDENCE.T function in Excel?
The CONFIDENCE.T function is one of the Statistical functions of Excel.
It Returns the confidence interval for a population mean, using a Student T distribution.
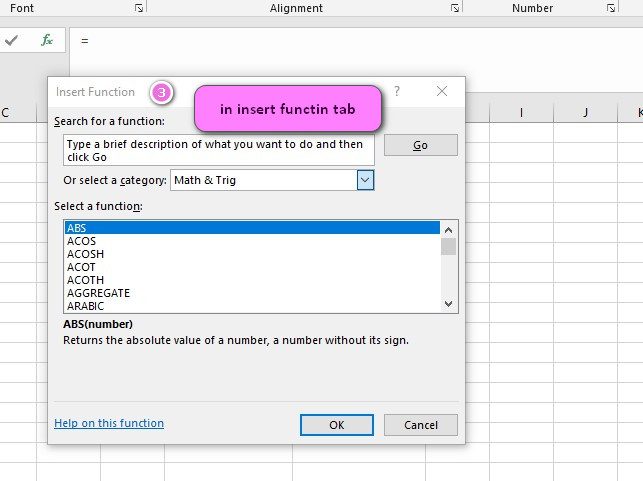
We can find this function in Statistical category of insert function Tab.
How to use CONFIDENCE.T function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
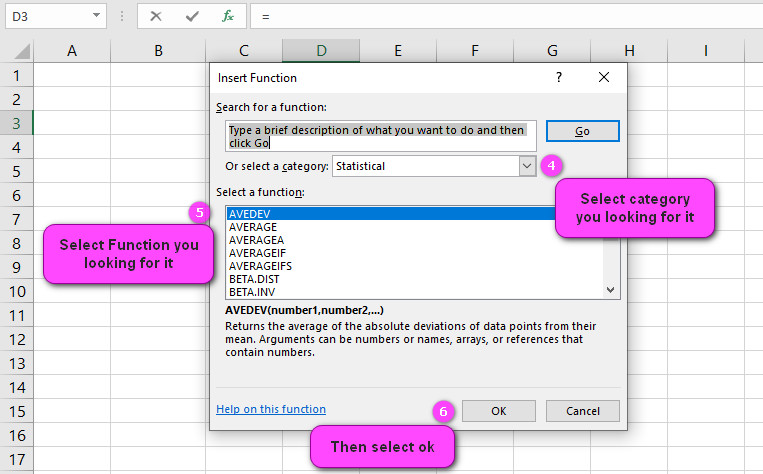
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select CONFIDENCE.T function.
6. Then select ok.
7. In the function arguments Tab you will see CONFIDENCE.T function.
8. Alpha is the significance level used to compute the confidence level, a number greater than 0 and less than 1.
9. Standard_dev is the population standard deviation for the data range and is assumed to be known. Standard_dev must be greater than 0.
10. Size is the sample size.
11. You will see the results in the formula result section.
Examples of CONFIDENCE.T function in Excel
- Calculating a 95% confidence interval for the population mean of a dataset of 50 observations with an unknown standard deviation: =CONFIDENCE.T(0.05,STDEV(A1:A50),COUNT(A1:A50))
- Calculating a two-tailed 99% confidence interval for the difference in means between two datasets of 20 and 25 observations respectively: =CONFIDENCE.T(0.005,STDEV(A1:A20,B1:B25),20+25-2)
- Estimating the sample size required to achieve a 90% confidence interval with a half-width of 0.5 given a population standard deviation of 2.5: =CEILING.MATH(((NORM.S.INV(0.05)*2.5)/0.5)^2,1)
- Calculating a one-tailed 97.5% confidence interval for the population proportion of successes in a dataset of 100 binary outcomes: =CONFIDENCE.T(0.025,SQRT(AVERAGE(A1:A100)*(1-AVERAGE(A1:A100))/100),100-1)
- Calculating a two-tailed 95% confidence interval for the population median of a dataset of 30 observations: =CONFIDENCE.T(0.025,STDEV(A1:A30)/(SQRT(COUNT(A1:A30))),COUNT(A1:A30)-1)
- Examining the significance of a multiple regression coefficient in a model with four predictors and 50 observations: =CONFIDENCE.T(0.05,STEYX(A1:A50,B1:B50,C1:C50,D1:D50,F1:F50),50-5)
- Evaluating the statistical significance of the interaction effect in a two-way ANOVA with three groups and 25 observations per group: =CONFIDENCE.T(0.05,STDEV(A1:A25,B1:B25,C1:C25),75-6)
- Calculating a two-tailed 98% confidence interval for the difference in means between two datasets of 15 and 20 observations respectively assuming equal variances: =CONFIDENCE.T(0.01,STDEV.P(A1:A15,B1:B20)*SQRT((1/15)+(1/20)),15+20-2)
- Estimating the sample size required to achieve a 99% confidence interval for the population mean with a half-width of 1.2 given an unknown standard deviation: =CEILING.MATH(((T.INV.2T(0.005,df)*STDEV(A1:A10))/1.2)^2,1)
- Calculating a one-tailed 95% confidence interval for the population standard deviation of a dataset of 40 observations assuming a normal distribution: =CONFIDENCE.T(0.05,STDEV(A1:A40),COUNT(A1:A40)-1)
Excel’s CONFIDENCE.T Function Explained: What It Is and How It Works
The CONFIDENCE.T function in Excel is used to calculate the confidence interval for a population mean, based on a sample size and a given level of confidence. The function returns two values – the lower and upper bounds of the confidence interval.
For example, let’s say you have a sample of 50 students and you want to calculate the 95% confidence interval for their average test score. You can use the CONFIDENCE.T function to do this by inputting the sample size (50), the standard deviation of the sample, and the desired confidence level (0.05) into the function.
The formula would look like this: =CONFIDENCE.T(0.05,STDEV(A1:A50),50)
This would return the lower and upper bounds of the confidence interval for the population mean, which you can interpret as the range within which you can be 95% confident that the true population mean lies.
How to Determine the Confidence Level for the CONFIDENCE.T Function in Excel
The confidence level for the CONFIDENCE.T function in Excel represents the probability that the true population mean lies within the calculated confidence interval. This value is typically expressed as a percentage, such as 90% or 95%.
To determine the confidence level for the function, simply subtract the desired level of significance from 1. For example, if you want a 95% confidence level, the level of significance would be 0.05 (1 – 0.95).
You can then input this level of significance into the CONFIDENCE.T function along with the other required arguments, as we demonstrated in the previous example.
Understanding the Required Arguments for Excel’s CONFIDENCE.T Function
The CONFIDENCE.T function in Excel requires three arguments: the level of significance, the standard deviation of the sample, and the size of the sample.
The level of significance is typically expressed as a decimal value, representing the probability of a type I error (rejecting a true null hypothesis). The standard deviation of the sample can be calculated using the STDEV function in Excel. Finally, the size of the sample represents the number of observations used to calculate the sample mean.
For example, if you want to calculate the 90% confidence interval for a sample of 100 measurements with a standard deviation of 2.5, you can use the following formula: =CONFIDENCE.T(0.1, 2.5, 100)
Can the CONFIDENCE.T Function Be Used with Non-Numerical Data in Excel?
No, the CONFIDENCE.T function in Excel can only be used with numerical data. If you try to use the function with non-numerical data, such as text or logical values, Excel will return the #NUM! error.
For example, let’s say you have a sample of student names and you want to calculate the confidence interval for their average test score. If you try to use the CONFIDENCE.T function with this data, you will receive the #NUM! error because the function cannot perform calculations on non-numerical data.
Calculating Standard Deviation for the CONFIDENCE.T Function in Excel
In order to use the CONFIDENCE.T function in Excel, you need to know the standard deviation of your sample. You can calculate this value using the STDEV function in Excel.
For example, let’s say you have a sample of 50 students and you want to calculate the confidence interval for their average test score. You can calculate the standard deviation of the sample using the following formula: =STDEV(A1:A50)
This would return the standard deviation of the sample, which you can then input into the CONFIDENCE.T function along with the other required arguments to calculate the confidence interval for the population mean.
CONFIDENCE.T vs. CONFIDENCE.NORM: What’s the Difference?
While both the CONFIDENCE.T and CONFIDENCE.NORM functions in Excel are used to calculate confidence intervals, they differ in their assumptions about the underlying population distribution.
The CONFIDENCE.T function assumes that the sample data follows a Student’s t-distribution, which is appropriate for small sample sizes or when the population standard deviation is unknown. On the other hand, the CONFIDENCE.NORM function assumes that the sample data follows a normal distribution, which is appropriate for large sample sizes or when the population standard deviation is known.
For example, if you have a sample size of 20 and want to calculate the 95% confidence interval for the population mean, you would use the CONFIDENCE.T function. However, if you have a sample size of 500 and know the population standard deviation, you would use the CONFIDENCE.NORM function instead.
Excel’s CONFIDENCE.T Function and Its Applicability for Small Sample Sizes
Excel’s CONFIDENCE.T function is particularly useful when working with small sample sizes, where the population standard deviation is unknown. This is because the function assumes that the sample data follows a Student’s t-distribution, which takes into account the additional uncertainty associated with estimating the population standard deviation from the sample data.
For example, let’s say you have a sample of 10 observations and want to calculate the 90% confidence interval for the population mean. You can use the CONFIDENCE.T function in Excel by inputting the level of significance (0.1), the standard deviation of the sample, and the size of the sample.
The formula would look like this: =CONFIDENCE.T(0.1,STDEV(A1:A10),10)
This would return the lower and upper bounds of the confidence interval for the population mean, which you can interpret as the range within which you can be 90% confident that the true population mean lies.
Using Excel’s CONFIDENCE.T Function for Two-Tailed Tests
The CONFIDENCE.T function in Excel can be used for both one-tailed and two-tailed tests. For a two-tailed test, simply divide the level of significance by 2 before inputting it into the function.
For example, let’s say you have a sample of 50 observations and want to perform a two-tailed test at the 95% confidence level. You can use the CONFIDENCE.T function in Excel with a level of significance of 0.025 (0.05/2).
The formula would look like this: =CONFIDENCE.T(0.025,STDEV(A1:A50),50)
This would return the lower and upper bounds of the confidence interval for the population mean, which you can interpret as the range within which you can be 95% confident that the true population mean lies.
How to Interpret the Result of Excel’s CONFIDENCE.T Function
The result of Excel’s CONFIDENCE.T function is a range of values that represents the confidence interval for the population mean. This range provides an estimate of the precision of your sample mean and indicates how much uncertainty there is surrounding the true population mean.
For example, if the result of the CONFIDENCE.T function is (45, 55), this means that you can be 95% confident that the true population mean lies somewhere between 45 and 55.
Excel’s CONFIDENCE.T Function for One-Sample and Two-Sample t-Tests
Excel’s CONFIDENCE.T function can be used for both one-sample and two-sample t-tests. For a one-sample t-test, the function calculates the confidence interval for the population mean based on a single sample. For a two-sample t-test, the function calculates the confidence interval for the difference between two population means, based on two independent samples.
For example, let’s say you want to conduct a one-sample t-test to determine if the average weight of a certain type of fruit is different from 100 grams. You can use the CONFIDENCE.T function to calculate the confidence interval for the population mean weight based on a sample of 20 fruits.
The formula would look like this: =CONFIDENCE.T(0.05,STDEV(A1:A20),20)
On the other hand, if you want to conduct a two-sample t-test to determine if there is a significant difference in the average weight of two types of fruit, you can use the CONFIDENCE.T function to calculate the confidence interval for the difference in population means based on two independent samples.
The formula would look like this: =CONFIDENCE.T(0.05,STDEV(A1:A20),20,STDEV(B1:B20),20)
The Maximum Sample Size Allowed for Excel’s CONFIDENCE.T Function
The maximum sample size allowed for Excel’s CONFIDENCE.T function is 32,767. This means that you can use the function to calculate the confidence interval for a population mean based on a sample of up to 32,767 observations.
For example, if you have a sample of 1,000 observations and want to calculate the 95% confidence interval for the population mean, you can use the CONFIDENCE.T function in Excel by inputting the level of significance (0.05), the standard deviation of the sample, and the size of the sample.
The formula would look like this: =CONFIDENCE.T(0.05,STDEV(A1:A1000),1000)
This would return the lower and upper bounds of the confidence interval for the population mean, which you can interpret as the range within which you can be 95% confident that the true population mean lies.
Accuracy of Results Obtained from Excel’s CONFIDENCE.T Function
The accuracy of results obtained from Excel’s CONFIDENCE.T function depends on the accuracy of the input data and the assumptions made about the underlying population distribution. If the sample size is large enough and the population standard deviation is known, the CONFIDENCE.NORM function may provide more accurate results than the CONFIDENCE.T function.
It’s also important to note that the confidence interval calculated using the CONFIDENCE.T function represents an estimate of the precision of the sample mean, but does not guarantee that the true population mean falls within the interval.
Setting the Alpha Value for Excel’s CONFIDENCE.T Function
The alpha value for Excel’s CONFIDENCE.T function represents the level of statistical significance of the test. It is typically set at 0.05 or 0.01, representing a 5% or 1% chance of rejecting a true null hypothesis, respectively.
To set the alpha value for the CONFIDENCE.T function in Excel, simply input the desired level of significance as a decimal value into the function.
For example, if you want to calculate the 95% confidence interval for a population mean based on a sample size of 50, you can use the CONFIDENCE.T function with an alpha value of 0.05 (1 – 0.95).
The formula would look like this: =CONFIDENCE.T(0.05,STDEV(A1:A50),50)
This would return the lower and upper bounds of the confidence interval for the population mean, which you can interpret as the range within which you can be 95% confident that the true population mean lies.
Calculating the Confidence Interval of a Population Proportion Using Excel’s CONFIDENCE.T Function
Excel’s CONFIDENCE.T function can also be used to calculate the confidence interval of a population proportion, such as the proportion of individuals who prefer a certain brand of product.
To do this, you need to input the sample size, the number of successes (such as the number of individuals who prefer the brand), and the desired confidence level as decimal values into the function.
For example, let’s say you have a sample of 200 individuals and 120 of them prefer a certain brand. You want to calculate the 90% confidence interval for the population proportion of individuals who prefer the brand.
The formula would look like this: =CONFIDENCE.T(0.1, SQRT((0.6*0.4)/200), 200, 1, 1)
This would return the lower and upper bounds of the confidence interval for the population proportion, which you can interpret as the range within which you can be 90% confident that the true population proportion lies.
Does Excel’s CONFIDENCE.T Function Assume a Normal Distribution?
The CONFIDENCE.T function in Excel assumes that the sample data follows a Student’s t-distribution, rather than a normal distribution. This is because the t-distribution takes into account the additional uncertainty associated with estimating the population standard deviation from the sample data.
However, for large sample sizes (typically above 30), the t-distribution becomes very similar to the normal distribution. In these cases, the CONFIDENCE.T and CONFIDENCE.NORM functions may provide very similar results.
Using Excel’s CONFIDENCE.T function for paired t-tests
The CONFIDENCE.T function in Excel can be used to calculate the confidence interval of a mean difference between paired samples. For example, let’s say we have data on the exam scores of 10 students before and after they received additional tutoring. We want to determine if the tutoring had a significant impact on their scores. We can use the paired t-test to compare the mean scores before and after tutoring and use the CONFIDENCE.T function to calculate the confidence interval of the mean difference.
Handling zero or negative standard deviations in Excel’s CONFIDENCE.T function
If the sample size is small and the standard deviation of the population is not known, the sample standard deviation may sometimes be zero or negative. In this case, the CONFIDENCE.T function returns the #DIV/0! error. To handle this error, we can add a small value to the sample standard deviation or use a different method to estimate the confidence interval, such as the t-distribution. For example, let’s say we have data on the height of 5 plants and the standard deviation of the population is unknown. The sample standard deviation is 0 because all the plants have the same height. We can add a small value, such as 0.1, to the sample standard deviation to avoid the #DIV/0! error.
Determining sample size for a specified margin of error using Excel’s CONFIDENCE.T function
The CONFIDENCE.T function can also be used to determine the sample size needed to achieve a specified margin of error with a given level of confidence. For example, let’s say we want to conduct a survey to estimate the proportion of people in a city who support a new policy proposal. We want the margin of error to be no more than 5% with 95% confidence. Using the CONFIDENCE.T function, we can calculate that a sample size of 385 is needed.
Calculating the confidence interval of a regression coefficient using Excel’s CONFIDENCE.T function
In addition to calculating the confidence interval of a mean difference or proportion, the CONFIDENCE.T function can also be used to calculate the confidence interval of a regression coefficient. For example, let’s say we have data on the salary and years of experience of employees in a company and we want to estimate the effect of years of experience on salary using linear regression. We can use the CONFIDENCE.T function with the appropriate degrees of freedom and level of confidence to calculate the confidence interval of the estimated regression coefficient.
Real-world applications of Excel’s CONFIDENCE.T function
The CONFIDENCE.T function is a useful tool for statistical analysis in various fields, such as business, finance, healthcare, and social science. For example, it can be used to analyze the impact of marketing campaigns on sales, evaluate the effectiveness of medical treatments, or assess the satisfaction of customers with a product or service. By providing a measure of uncertainty around a point estimate, the confidence interval can help decision-makers make informed choices based on the available data.
CONFIDENCE.T related functions
- Use CONFIDENCE.NORM to return the confidence interval for a population mean, using a normal distribution.