What is CORREL function in Excel?
The CORREL function is one of the Statistical functions of Excel.
It Returns the correlation coefficient between two data sets.
We can find this function in Statistical category of the insert function Tab.
How to use CORREL function in excel
- Click on an empty cell (like F5).
2. Click on the fx icon (or press shift+F3).
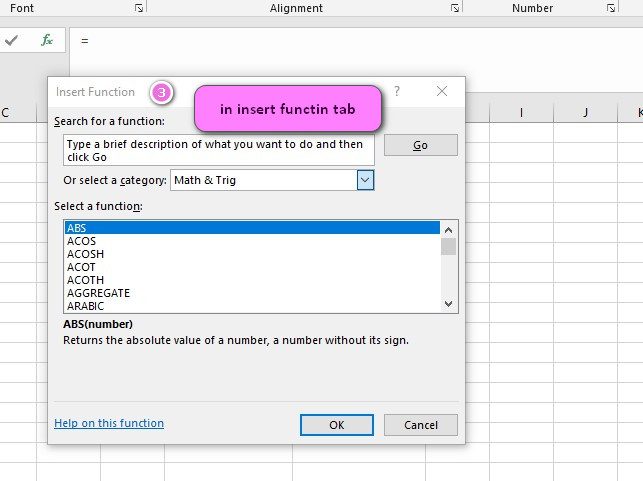
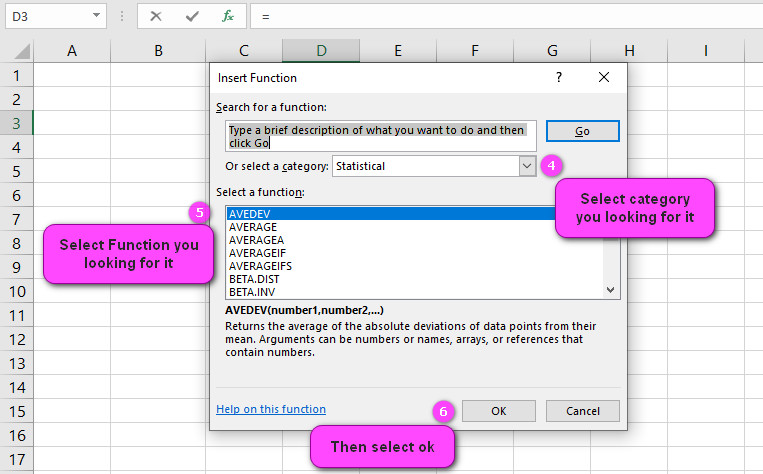
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select CORREL function.
6. Then select ok.
7. In the function arguments Tab you will see CORREL function.
8. Array1 is a cell range of values. The values should be numbers, names, arrays, or references that contain numbers.
9. Array2 is a second cell range of values. The values should be numbers, names, arrays, or references that contain numbers.

10. You will see the results in the formula result section.
MATH of CORREL function in Excel
example1:
what is the formula for the correlation coefficient in excel?
Here is the formula for the correlation coefficient:

example 2:
How to calculate the correlation coefficient in Excel?

=SUM((B2:B10-AVERAGE(B2:B10))*(C2:C10-AVERAGE(C2:C10)))/SQRT(SUM((B2:B10-AVERAGE(B2:B10))^2)*SUM((C2:C10-AVERAGE(C2:C10))^2))The process for finding the mean absolute deviation involves the following steps.
1.get numbers.
Age=25,25,27,22,29,29,21,25,22
Height=210,205,195,198,199,201,202,200,2042. calculate average of numbers.
=AVERAGE(B2:B10)----->>>>answer is 25
=AVERAGE(C2:C10)----->>>>answer is 201.553. calculate distance from average of numbers.
=AVERAGE(B2:B10)-B11----->>>>answer is
0,0,2,-3,4,4,-4,0,-3
=AVERAGE(B2:B10)-C11----->>>>answer is 8.4,3.4,-6.5,-3.5,-2.5,-0.5,0.4,-1.5,2.44. calculate the power of distance from average of numbers.
=(B2:B10-AVERAGE(B2:B10))^2----->>>>answer is
0,0,4,9,16,16,16,0,9
=(C2:C10-AVERAGE(C2:C10))^2----->>>>answer is 71.3,11.86,42.97,12.64,6.53,0.3,0.19,2.415.975. calculate the product of distance from average of numbers.
=(AVERAGE(B2:B10)-B11) *(AVERAGE(B2:B10)-C11)----->>>>answer is
0,0,-13.1,10.6,-10.2,-2.2,-1.7,0,-7.36. Finally calculate the correlation coefficient.
=SUM((B2:B10-AVERAGE(B2:B10))*(C2:C10-AVERAGE(C2:C10)))/SQRT(SUM((B2:B10-AVERAGE(B2:B10))^2)*SUM((C2:C10-AVERAGE(C2:C10))^2))----->>>>answer is -0.23All these steps are summarized in the following function.
Examples of CORREL function in Excel
here are 10 examples of the CORREL function in Excel:
- To find the correlation coefficient between two sets of data, use the formula “=CORREL(A2:A10, B2:B10)” where A2:A10 and B2:B10 are the ranges of data.
- You can also reference named ranges like this: “=CORREL(Sales, Expenses)” where “Sales” and “Expenses” are named ranges for the data.
- If you want to calculate the correlation coefficient for a larger dataset, use the formula “=CORREL(A2:A1000, B2:B1000)” (or adjust the ranges as needed).
- The CORREL function works with non-numeric data as well. For example, “=CORREL(A2:A10, C2:C10)” would calculate the correlation between two columns of text values.
- You can use the CORREL function to find the correlation between more than two sets of data. For example, “=CORREL(A2:A10, B2:B10, C2:C10)” would calculate the correlation between three ranges of data.
- The correlation coefficient calculated by CORREL ranges from -1 to 1. If the result is close to -1, it indicates a strong negative correlation; if close to 1, a strong positive correlation. A result close to 0 means little or no correlation.
- You can use the ABS function to ignore the sign of the correlation coefficient. For example, “=ABS(CORREL(A2:A10, B2:B10))” would give the same result as “=CORREL(A2:A10, B2:B10)” but without the negative sign.
- If you have missing data in one set of data, you can use the IFERROR function to exclude that data from the calculation. For example, “=CORREL(A2:A10, IFERROR(B2:B10, “”))” would ignore any blank cells in the second range.
- You can use the CORREL function with array formulas to calculate several correlations at once. For example, “=CORREL(A2:A10, B2:B10:E2:E10)” would give a correlation matrix comparing the first set of data to the other three sets.
- Finally, you can use the CORREL function in combination with other statistical functions like AVERAGE or STDEV to analyze complex datasets. For example, “=CORREL(A2:A100, AVERAGE(B2:B100), STDEV(C2:C100))” would calculate the correlation between the first set of data and the mean and standard deviation of two other ranges.
Errors in CORREL function
If you enter a non-numeric number, the output show #DIV/0! or #NAME? error
CORREL(a,b) ----->>>>answer is #NAME?
CORREL("a","b") ----->>>>answer is #DIV/0!
Using the CORREL Function in Excel
To use the CORREL function in Excel, you will need to provide the range of values for two sets of variables that you want to calculate the correlation coefficient for.
Simply enter “=CORREL(array1,array2)” into a cell and replace “array1” and “array2” with your own ranges of data.
For example, let’s say you have two sets of data in columns A and B, and you want to calculate the correlation coefficient between these two sets of data.
You would enter the following formula into an empty cell:
=CORREL(A1:A10,B1:B10)
Then press “Enter”, and the result will appear in that cell.
Syntax for the CORREL Function in Excel
The syntax for the CORREL function in Excel is as follows: “=CORREL(array1,array2)”, where “array1” and “array2” represent the two sets of variables for which you want to calculate the correlation coefficient.
As an example, suppose you have two sets of data: “X” and “Y”.
To calculate the correlation coefficient between these two sets of data using the CORREL function, you would enter “=CORREL(X,Y)” into a cell.
Calculating Correlation Coefficients for Non-linear Relationships
The CORREL function in Excel can only calculate the correlation coefficient for linear relationships and cannot be used for non-linear relationships.
For non-linear relationships, other statistical methods such as polynomial regression or Spearman’s rank correlation coefficient may be used instead.
For instance, suppose you have a set of data that follows a curved pattern, such as an exponential or logarithmic curve.
In this case, you could try plotting the data on a scatter plot to visualize the relationship between the variables and determine if there is a linear or non-linear relationship present.
Handling Missing Data in Excel with the CORREL Function
The CORREL function in Excel can handle missing data by ignoring any cells that contain a missing or null value.
For example, if you have a dataset where some cells are blank or contain the value “#N/A”, the CORREL function will exclude these cells from the calculation.
As an example, suppose you have two sets of data: “X” and “Y”. Some of the cells in the “Y” range are missing values.
To use the CORREL function, you would enter “=CORREL(X,Y)” into a cell. The function will automatically exclude the missing cells in the “Y” range from the calculation.
Comparing Multiple Sets of Data with the CORREL Function
The CORREL function in Excel can only compare two sets of data at a time. If you want to compare more than two sets of data, you will need to use an array formula along with the CORREL function.
For example, let’s say you have three sets of data in columns A, B, and C, from rows 1 to 10.
To calculate the correlation coefficients between all three sets of data, you would enter the following formula into an empty cell:
{=CORREL(A1:A10,B1:B10,C1:C10)}
Note that this is an array formula, so instead of pressing “Enter” after typing in the formula, you need to press “Ctrl+Shift+Enter”. This will return an array of correlation coefficients for each pair of sets of data.
Range of Values Returned by the CORREL Function in Excel
The range of values returned by the CORREL function in Excel is between -1 and 1. A value of -1 indicates a perfect negative correlation, a value of 0 indicates no correlation, and a value of 1 indicates a perfect positive correlation.
For example, if the result of the CORREL function is -0.8, this means that there is a strong negative correlation between the two sets of data being compared.
Limitations of the CORREL Function in Excel
There is no specific limit to the number of data points that can be used with the CORREL function in Excel.
However, as the number of data points increases, the calculation may become slower and more resource-intensive.
Additionally, the CORREL function can only be used to calculate the correlation coefficient for linear relationships, not non-linear ones.
If you have a non-linear relationship between two sets of data, you may need to use a different statistical method to analyze the relationship.
Interpreting the Output of the CORREL Function in Excel
The output of the CORREL function in Excel is a correlation coefficient that indicates the strength and direction of the relationship between two sets of data.
A value of 1 indicates a perfect positive correlation, meaning that as one variable increases, the other variable also increases.
A value of -1 indicates a perfect negative correlation, meaning that as one variable increases, the other variable decreases.
A value of 0 indicates no correlation, meaning that the two variables are not related to each other. The closer the correlation coefficient is to -1 or 1, the stronger the correlation between the two variables.
Calculating Partial Correlations
The CORREL function in Excel cannot be used to calculate partial correlations.
However, you can use other statistical methods such as multiple regression analysis or covariance analysis to calculate partial correlations.
Calculating the Significance of the Correlation Coefficient
The CORREL function in Excel does not provide a direct measure of the significance of the correlation coefficient. However, you can calculate the significance level using hypothesis testing.
One common method is to use a t-test to determine if the correlation coefficient is significantly different from zero.
For example, suppose you have calculated a correlation coefficient using the CORREL function in cell A1. To test the significance of the correlation coefficient, you could use the following formula:
=T.TEST(array1,array2,2,1)
where “array1” and “array2” are the two sets of data used to calculate the correlation coefficient, 2 represents the number of tails for the test, and 1 represents the type of t-test (two-sample assuming equal variances).
The result of the T.TEST function will give you a p-value, which represents the probability that the observed correlation coefficient is due to chance.
The lower the p-value, the greater the evidence against the null hypothesis (i.e., no correlation).
Assumptions of Causality and the CORREL Function in Excel
Using the CORREL function in Excel does not assume a causal relationship between the two sets of data being compared.
Instead, the function only calculates the strength and direction of the linear relationship between the two sets of data.
It’s important to note that correlation does not imply causation. Just because two variables are correlated does not necessarily mean that one causes the other.
There may be other factors at play that influence both variables.
Calculating Spearman’s Rank Correlation Coefficient
The CORREL function in Excel can be used to calculate Spearman’s rank correlation coefficient by ranking the data before calculating the correlation coefficient.
To do this, you can use the RANK or RANK.EQ function to assign ranks to the data, and then use the CORREL function to calculate the correlation coefficient.
For example, suppose you have two sets of data in columns A and B, and you want to calculate the Spearman’s rank correlation coefficient between these two sets of data.
You would enter the following formula into an empty cell:
=CORREL(RANK(A1:A10),RANK(B1:B10))
Then press “Enter”, and the result will appear in that cell. The RANK function assigns a rank to each value in the range, so the CORREL function can calculate the rank correlation coefficient.
Calculating the Pearson Correlation Coefficient for Grouped Data
To calculate the Pearson correlation coefficient for grouped data using the CORREL function in Excel, you need to calculate the midpoint of each group and use those values as inputs for the function.
The formula for calculating the midpoint is:
Midpoint = (Lower Limit + Upper Limit) / 2
Once you have calculated the midpoints for each group, you can use the CORREL function to calculate the correlation coefficient between the two sets of data.
For example, suppose you have two sets of grouped data in columns A and B, and you want to calculate the Pearson correlation coefficient between these two sets of data.
You would first calculate the midpoint for each group in column C using the formula “= (A2+A3)/2” and “= (B2+B3)/2”, and so on, down to the last row.
Then, enter the following formula into an empty cell:
=CORREL(C2:C10,D2:D10)
Then press “Enter”, and the result will appear in that cell.
Calculating the Correlation Coefficient for Time Series Data
The CORREL function in Excel can be used to calculate the correlation coefficient for time series data by treating the time series as a set of ordered pairs.
Simply enter the time series data into two separate columns, with the time stamps in column A and the corresponding measurements in column B.
Then, use the CORREL function as usual to calculate the correlation coefficient.
For example, let’s say you have time series data for two variables in columns A and B, with the time stamp in column A and the measurement in column B.
To calculate the correlation coefficient between these two variables using the CORREL function, you would simply enter the following formula into an empty cell:
=CORREL(B2:B100,C2:C100)
Then press “Enter”, and the result will appear in that cell.
Calculating the p-value for the Correlation Coefficient
The CORREL function in Excel does not directly provide a p-value for the correlation coefficient.
However, you can use the T.TEST function to calculate the p-value based on the correlation coefficient and the sample size.
For example, suppose you have two sets of data in columns A and B, and you have calculated the correlation coefficient using the CORREL function in cell C1.
To calculate the p-value for this correlation coefficient, you would enter the following formula into an empty cell:
=T.TEST(A1:A100,B1:B100,2,1)
This formula uses the T.TEST function to calculate the two-tailed p-value for a t-test based on the two sets of data and the type of test (two-sample assuming equal variances).
The result of the formula is the p-value associated with the correlation coefficient in cell C1.
Known Issues and Limitations of the CORREL Function in Excel
One known limitation of the CORREL function in Excel is that it can only be used to calculate the correlation coefficient for linear relationships and cannot be used for non-linear relationships.
Additionally, the function assumes that the data is normally distributed and that outliers are rare.
Another issue to be aware of is that the correlation coefficient measures only the strength and direction of the linear relationship between two variables, but it cannot determine causality.
Therefore, interpretation of the results must be done with care, and additional analysis may be required to establish causation.
Using the CORREL Function with Arrays in Excel
The CORREL function in Excel can be used with arrays to calculate the correlation coefficient between multiple sets of data.
To use the CORREL function with arrays, you simply need to enter the ranges of data as arrays in the formula.
For example, suppose you have three sets of data in columns A, B, and C, from rows 1 to 10.
To calculate the correlation coefficients between all three sets of data using arrays, you would enter the following formula into an empty cell:
=CORREL(A1:A10,B1:B10:C1:C10)
Note that this is a single formula that includes all three sets of data as separate arrays separated by colons. The result will be an array of correlation coefficients for each pair of sets of data.
Comparing Non-Numerical Sets of Data with the CORREL Function in Excel
The CORREL function in Excel can only be used to compare numerical sets of data. It cannot be used to compare non-numerical sets of data, such as text strings.
If you want to compare non-numerical sets of data, you will need to convert them into numerical values first.
For example, if you have categorical data, you could assign numerical codes to each category and then use those codes as inputs for the CORREL function.
Calculating an Adjusted Correlation Coefficient
To calculate an adjusted correlation coefficient in Excel using the CORREL function, you need to adjust the formula based on the sample size and the number of variables being compared.
The formula for the adjusted correlation coefficient is:
Adjusted r = r * sqrt((n – k – 1) / (n – 2))
where “r” is the unadjusted correlation coefficient, “n” is the sample size, and “k” is the number of variables being compared.
For example, suppose you have two sets of data in columns A and B, and you want to calculate the adjusted correlation coefficient using the CORREL function.
You would first calculate the unadjusted correlation coefficient using the formula “=CORREL(A1:A10,B1:B10)“, and then use the above formula to calculate the adjusted correlation coefficient.
Detecting Outliers with the CORREL Function in Excel
The CORREL function in Excel does not have built-in functionality for detecting outliers in a data set.
However, you can manually identify outliers by visually inspecting the scatter plot of the data or by using statistical methods such as the Z-score or interquartile range (IQR).
Once you identify the outliers, you may choose to remove them from the data set before calculating the correlation coefficient using the CORREL function.
This can help to improve the accuracy of the result and eliminate any spurious correlations that may be caused by outliers.