What is KURT function in Excel?
The KURT function is one of the Statistical functions of Excel.
It returns the Kurtosis of a data set.
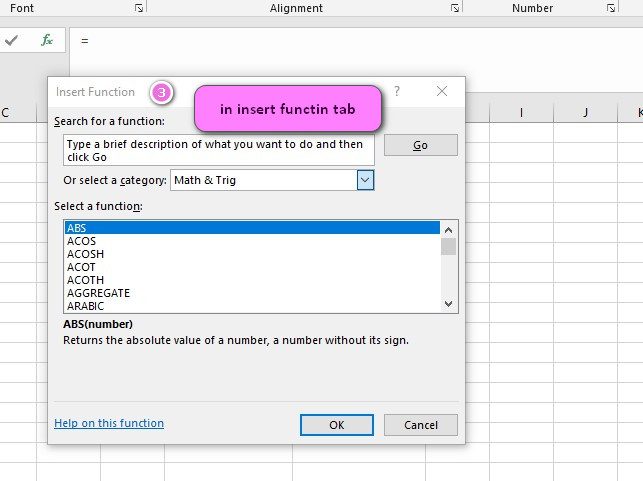
We can find this function in Statistical category of insert function Tab.
How to use KURT function in excel
- Click on an empty cell (like F5).
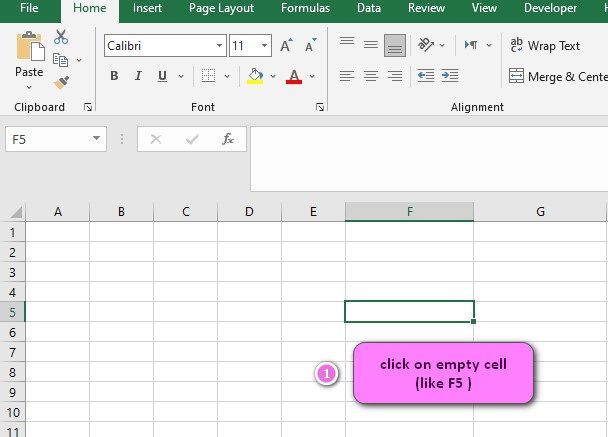
2. Click on the fx icon (or press shift+F3).
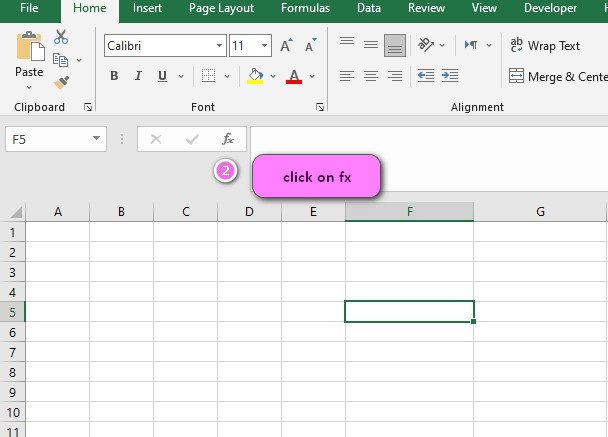
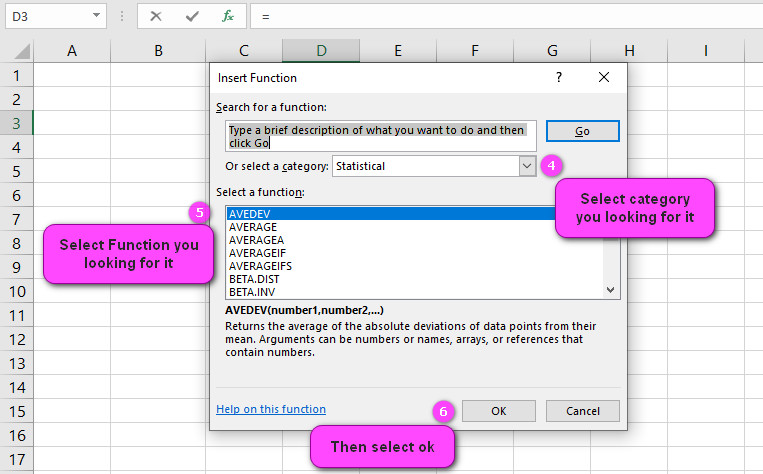
3. In the insert function tab you will see all functions.
4. Select STATISTICAL category.
5. Select KURT function.
6. Then select ok.
7. In the function arguments Tab you will see KURT function.
8. Number1: number1,number2,… are 1 to 255 numbers or names, arrays, or references that contain numbers for which you want the kurtosis.
9. Number2: number1,number2,… are 1 to 255 numbers or names, arrays, or references that contain numbers for which you want the kurtosis.
10. You will see the results in the formula result section.
Examples of KURT function in Excel
here are ten examples of the KURT function in Excel:
- Calculate the kurtosis of a range of data:
=KURT(A1:A10) - Calculate the excess kurtosis of a range of data:
=KURT(A1:A10)-3 - Calculate the kurtosis of a named range:
=KURT(MyData) - Calculate the kurtosis of a range of data, ignoring text values:
=KURT(IF(ISNUMBER(A1:A10),A1:A10)) - Calculate the kurtosis of a range of data, treating zeroes as missing values:
=KURT(IF(A1:A10<>0,A1:A10)) - Calculate the kurtosis of a range of data, treating negative values as missing values:
=KURT(IF(A1:A10>=0,A1:A10)) - Calculate the kurtosis of a range of data, treating outliers as missing values:
=KURT(IF(ABS(A1:A10-MEDIAN(A1:A10))<=3*STDEV(A1:A10),A1:A10)) - Calculate the kurtosis of a range of data, treating extreme outliers as missing values:
=KURT(IF(ABS(A1:A10-MEDIAN(A1:A10))<=2*QUARTILE(A1:A10,3)-QUARTILE(A1:A10,1),A1:A10)) - Calculate the kurtosis of a range of data, treating extreme positive and negative values as missing values:
=KURT(IF(AND(A1:A10>=QUARTILE(A1:A10,0.25),A1:A10<=QUARTILE(A1:A10,0.75)),A1:A10)) - Calculate the kurtosis of a range of data, treating values outside a specified range as missing values:
=KURT(IF(AND(A1:A10>=0,A1:A10<=100),A1:A10))
What does the KURT function in Excel do?
The KURT function in Excel is used to calculate the kurtosis of a data set. Kurtosis is a statistical measure that quantifies how much a distribution deviates from a normal distribution. A positive kurtosis indicates that a distribution has more extreme values than a normal distribution, while a negative kurtosis indicates that a distribution has fewer extreme values than a normal distribution.
The syntax for the KURT function is:
KURT(number1, [number2], …)
Where:
- number1, number2, … are the values or ranges containing the data you want to calculate the kurtosis for.
Here’s an example of how to use the KURT function in Excel:
Suppose you have a data set of 10 numbers: 5, 7, 8, 9, 10, 12, 15, 20, 25, and 30. You can use the KURT function to calculate the kurtosis of this data set as follows:
- Select a cell where you want to display the result, let’s say A1.
- Enter the formula “=KURT(A2:A11)” into cell A1 (assuming that the data set is in cells A2 through A11).
- Press Enter.
The result should be 0.2536, which indicates that the data set is slightly more peaked than a normal distribution.
Another example is a data set with the following values: 1, 2, 3, 4, 5, 6, 7, 8, 9, and 10.
If you calculate the kurtosis of this data set using the KURT function, the result would be -1.2361, which indicates that the data set has fewer extreme values than a normal distribution.
In general, a kurtosis value between -1 and 1 is considered normal, while a value greater than 1 indicates a more peaked distribution and a value less than -1 indicates a flatter distribution.
How is the kurtosis of a distribution defined?
Kurtosis is a statistical measure that describes the degree of peakedness or flatness of a probability distribution.
In Excel, the kurtosis of a dataset can be calculated using the KURT function. The syntax for the KURT function is as follows:
KURT(number1, [number2], ...)
where number1, number2, etc. are the values in the dataset.
The KURT function returns the kurtosis of the dataset. A positive kurtosis value indicates a more peaked distribution (leptokurtic), while a negative kurtosis value indicates a flatter distribution (platykurtic).
A value of zero indicates a normal distribution (mesokurtic).
Here’s an example: suppose we have a dataset of exam scores for a class of 30 students. We can calculate the kurtosis of this dataset using the KURT function as follows:
=KURT(A1:A30)
where A1:A30 contains the exam scores. If the resulting value is greater than zero, then the distribution of exam scores is more peaked than a normal distribution, meaning that there are more scores clustered around the mean.
If the resulting value is less than zero, then the distribution of exam scores is flatter than a normal distribution, meaning that there are fewer scores clustered around the mean.
For example, if the resulting value is 2, then the distribution of exam scores is leptokurtic, indicating that there are more scores clustered around the mean compared to a normal distribution.
Conversely, if the resulting value is -2, then the distribution of exam scores is platykurtic, indicating that there are fewer scores clustered around the mean compared to a normal distribution.
How do I use the KURT function in a formula?
The KURT function in Excel is used to calculate the kurtosis of a range or array of values.
Kurtosis is a measure of the shape of a distribution, specifically, how peaked or flat it is compared to a normal distribution.
To use the KURT function in a formula in Excel, follow these steps:
- Select the cell where you want to display the result.
- Type “=” (without quotes) to begin the formula.
- Type “KURT(” (without quotes) to start the KURT function.
- Select the range or array of values for which you want to calculate the kurtosis. You can do this by clicking and dragging over the cells, or by typing the cell range manually, such as A1:A10.
- Close the parentheses by typing “)” (without quotes).
- Press Enter to calculate the kurtosis.
Here’s an example: let’s say you have a set of data representing the heights of 10 people:
| Person | Height |
|---|---|
| 1 | 62 |
| 2 | 65 |
| 3 | 68 |
| 4 | 71 |
| 5 | 74 |
| 6 | 77 |
| 7 | 80 |
| 8 | 83 |
| 9 | 86 |
| 10 | 89 |
To calculate the kurtosis of this data using the KURT function, select a cell where you want to display the result, such as B2. Then, type the following formula:
=KURT(B2:B11)
This will calculate the kurtosis of the height data and display the result in the selected cell.
Note that in this example, we included an extra row above the data to label the columns.
When selecting the range of values for the KURT function, we included an extra row at the bottom to exclude the column label from the calculation.
What values can be returned by the KURT function?
The KURT function in Excel is used to calculate the kurtosis of a set of data, which is a measure of the peakedness and tail heaviness of a distribution compared to a normal distribution.
The function returns a numeric value that represents the kurtosis of the supplied data.
The values that can be returned by the KURT function are as follows:
- If the kurtosis value is positive, it indicates that the distribution of the data is more peaked than a normal distribution, and has heavier tails. This type of distribution is called a leptokurtic distribution.
Example: Suppose you have a set of data for the weights of 1000 people, and the KURT function returns a value of 2.5. This means that the distribution of weights is more peaked than a normal distribution, and has heavier tails.
- If the kurtosis value is negative, it indicates that the distribution of the data is less peaked than a normal distribution, and has lighter tails. This type of distribution is called a platykurtic distribution.
Example: Suppose you have a set of data for the heights of 500 people, and the KURT function returns a value of -1.2. This means that the distribution of heights is less peaked than a normal distribution, and has lighter tails.
- If the kurtosis value is zero, it indicates that the distribution of the data is similar to a normal distribution.
Example: Suppose you have a set of data for the test scores of 200 students, and the KURT function returns a value of 0. This means that the distribution of test scores is similar to a normal distribution.
- It is also possible for the KURT function to return an error value if the input data set is empty or contains only one data point.
Example: If you try to calculate the kurtosis of a data set with only one value, the KURT function will return an error.
In summary, the KURT function in Excel returns a numeric value that represents the kurtosis of a set of data, and this value can be positive, negative or zero depending on the shape of the distribution.
Can the KURT function be used for both sample and population data?
the KURT function in Excel can be used for both sample and population data.
The KURT function is used to calculate the kurtosis of a data set, which measures the degree of peakedness or flatness of the distribution compared to a normal distribution.
When using the KURT function in Excel, you need to specify whether the data represents a sample or a population.
If the data represents a sample, you should use the KURT.S function, and if it represents a population, you should use the KURT.P function.
Here are some examples to help illustrate the use of these functions:
Example 1: Suppose we have a sample of 10 test scores: 85, 90, 80, 75, 95, 100, 70, 80, 85, 90. To calculate the kurtosis of this sample using the KURT.S function, we would enter the following formula into a cell: =KURT.S(A1:A10). This returns a kurtosis value of -0.772, indicating that the distribution of test scores is relatively flat compared to a normal distribution.
Example 2: Suppose we have a population of 20 salaries: $50,000, $60,000, $70,000, $80,000, $90,000, $100,000, $110,000, $120,000, $130,000, $140,000, $150,000, $160,000, $170,000, $180,000, $190,000, $200,000, $210,000, $220,000, $230,000, $240,000. To calculate the kurtosis of this population using the KURT.
P function, we would enter the following formula into a cell: =KURT.P(A1:A20). This returns a kurtosis value of -1.121, indicating that the distribution of salaries is relatively peaked compared to a normal distribution.
In both examples, notice that we used different versions of the KURT function depending on whether the data represented a sample or a population.
Therefore, it is important to correctly specify which version of the function to use, depending on the type of data you are working with.
How does the KURT function handle errors or empty cells?
In Excel, the KURT function is used to calculate the kurtosis of a data set. Kurtosis measures the degree of peakedness or flatness of a distribution.
A high kurtosis indicates a highly peaked distribution, while a low kurtosis indicates a flatter distribution.
When it comes to handling errors or empty cells in the KURT function, Excel follows certain rules:
- If the input range contains text or logical values, the KURT function returns the #VALUE! error.
- If the input range has fewer than four values, the KURT function returns the #DIV/0! error.
- If the input range has exactly four values, the KURT function returns 0.
- If the input range has more than four values, the KURT function calculates the kurtosis of the data set.
Let’s take a look at some examples:
Example 1: Suppose you have the following data set in cells A1:A6: 5, 9, 6, “”, 8, 7 The empty cell represents a blank cell.
If you use the formula =KURT(A1:A6), Excel returns the #VALUE! error because the input range contains an empty cell.
Example 2: Suppose you have the following data set in cells A1:A3: 3, 4, 5
If you use the formula =KURT(A1:A3), Excel returns the #DIV/0! error because the input range has fewer than four values.
Example 3: Suppose you have the following data set in cells A1:A4: 10, 20, 30, 40
If you use the formula =KURT(A1:A4), Excel returns -1.2 because the input range has more than four values and the kurtosis of this data set is negative, indicating a flatter distribution.
Example 4: Suppose you have the following data set in cells A1:A5: 5, 10, 15, 20, 25
If you use the formula =KURT(A1:A5), Excel returns -1.3 because the input range has more than four values and the kurtosis of this data set is negative, indicating a flatter distribution.
In summary, the KURT function handles errors or empty cells in Excel by returning an error message if the input range contains text or logical values, or if it has less than four values.
If the input range has exactly four values, the KURT function returns 0. Otherwise, it calculates the kurtosis of the data set.
How accurate is the KURT function in Excel?
The KURT function in Excel is used to calculate the kurtosis of a dataset, which is a measure of how peaked or flat its distribution is compared to the normal distribution.
The function returns the excess kurtosis, which is calculated as the fourth moment of the dataset divided by the square of the variance minus 3.
The KURT function can be accurate for datasets that follow a normal distribution, but it may not be appropriate for non-normal distributions.
In addition, the accuracy of the KURT function can be affected by the sample size of the dataset. For small sample sizes, the kurtosis estimate can be highly variable and less reliable.
Here’s an example of using the KURT function in Excel:
Suppose we have a dataset of exam scores:
| Score |
|---|
| 80 |
| 85 |
| 90 |
| 95 |
| 100 |
To find the kurtosis of this dataset using the KURT function, we can enter the following formula into a cell:
Copy Code=KURT(A2:A6)
This will return the value of 1.52, which indicates that the dataset is moderately peaked compared to a normal distribution.
However, if we have a different dataset that follows a non-normal distribution, such as a skewed or bimodal distribution, the kurtosis estimate from the KURT function may not accurately reflect the shape of the dataset.
In summary, while the KURT function in Excel can provide a measure of kurtosis for a dataset, its accuracy depends on the underlying distribution and sample size of the data.
It is important to interpret the kurtosis estimate in the context of the specific dataset being analyzed.
Can the KURT function be used with non-numeric data?
the KURT function in Excel can only be used with numeric data.
The function is designed to calculate the kurtosis of a distribution or dataset, which is a statistical measure that describes the shape of the distribution.
Kurtosis is a measure of the “peakedness” or “flatness” of a distribution compared to the normal distribution.
A kurtosis value of zero indicates that the distribution has the same shape as the normal distribution, while positive values indicate a more peaked distribution (i.e., tall and thin) and negative values indicate a flatter distribution (i.e., short and wide).
The KURT function in Excel can be used to calculate the kurtosis of a range of data.
For example, if you have a range of data in cells A1:A10, you could use the following formula to calculate the kurtosis:
=KURT(A1:A10)
However, if any non-numeric data is included in the range, the function will return the #VALUE! error message.
For instance, if cell A5 contains a text string like “N/A” or an empty cell, the formula above would return the #VALUE! error message.
This is because the function cannot calculate the kurtosis of non-numeric values.
In summary, the KURT function in Excel can only be used with numeric data and will not work with non-numeric data.
Are there any alternatives to the KURT function in Excel?
there are alternatives to the KURT function in Excel. The KURT function is used to calculate the kurtosis of a data set, which is a measure of the “peakedness” or “flatness” of the distribution.
One alternative is the SKEW function, which calculates the skewness of a data set. Skewness is a measure of the asymmetry of the distribution.
A positive skew indicates that the distribution has a tail on the right side, while a negative skew indicates a tail on the left side. The SKEW function can be used as follows:
=SKEW(data_range)
For example, if you have a data set in cells A1:A10, you would enter:
=SKEW(A1:A10)
Another alternative is to use the descriptive statistics tool in Excel. This tool provides a range of statistical measures, including kurtosis and skewness.
To access the tool, select the data range and then click on “Data” in the menu bar. From there, select “Data Analysis” and then “Descriptive Statistics.”
In the dialog box that appears, make sure “Summary statistics” is selected and check the boxes for “Kurtosis” and “Skewness.” Click “OK” and Excel will generate a table with the requested statistics.
Here’s an example: suppose you have a set of data representing the heights of students in a class. The data is in cells A1:A10. To calculate the skewness using the SKEW function, you would enter:
=SKEW(A1:A10)
To use the descriptive statistics tool instead, you would follow these steps:
- Select the data range (A1:A10)
- Click on “Data” in the menu bar
- Select “Data Analysis”
- Select “Descriptive Statistics” and click “OK”
- In the dialog box that appears, make sure “Summary statistics” is selected
- Check the boxes for “Kurtosis” and “Skewness”
- Click “OK”
Excel will generate a table with the requested statistics.
How do I interpret the result of the KURT function?
The KURT function in Excel is used to calculate the kurtosis of a dataset. Kurtosis is a measure of the shape of a distribution, specifically how peaked or flat it is compared to a normal distribution.
The KURT function takes one or more numeric values as input and returns the kurtosis of the dataset.
A positive kurtosis value indicates a peakier distribution than a normal distribution, while a negative kurtosis value indicates a flatter distribution than a normal distribution.
Here’s an example: suppose you have a dataset of 10 values: {2, 4, 6, 8, 10, 12, 14, 16, 18, 20}. To calculate the kurtosis of this dataset in Excel, you would use the formula “=KURT(A1:A10)” assuming the data is located in cells A1 through A10.
The result of this formula would be -1.23 which indicates that the distribution is slightly flatter than a normal distribution.
Another example would be a dataset with the following 10 values: {-3, -2, -1, 0, 1, 2, 3, 4, 5, 6}. To calculate the kurtosis of this dataset in Excel, you would use the formula “=KURT(A1:A10)” where the data is located in cells A1 through A10.
The result of this formula would be 1.78 which indicates that the distribution is more peaked than a normal distribution.
In general, a kurtosis value close to zero indicates that the distribution is similar to a normal distribution, while a kurtosis value far from zero indicates a distribution that differs from a normal distribution in terms of its shape.
However, it’s important to note that the interpretation of kurtosis depends on the context of the dataset being analyzed.