What is LOGNORM.DIST function in Excel?
The LOGNORM.DIST function is one of the Statistical functions of Excel.
It returns the lognormal distribution of x, where In(y) is normally distributed
with parameters Mean and Standard_dev.
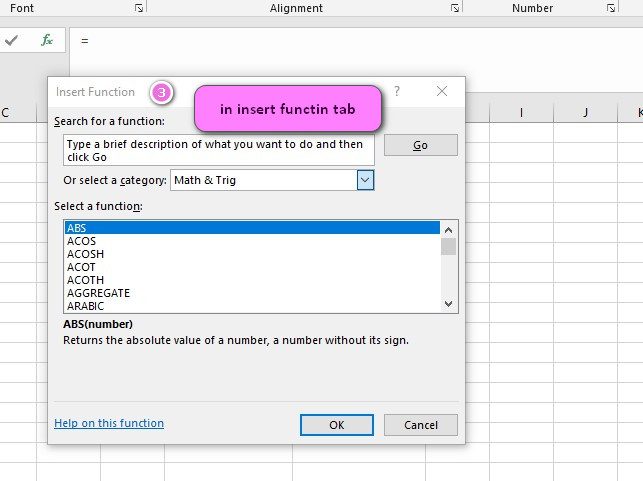
We can find this function in Statistical of insert function Tab.
How to use LOGNORM.DIST function in excel
- Click on an empty cell (like F5).
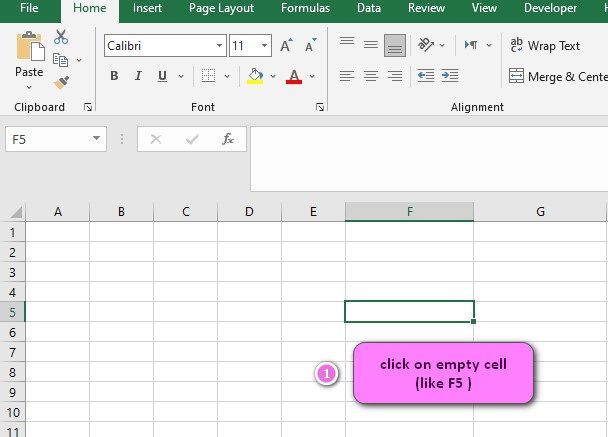
2. Click on the fx icon (or press shift+F3).
3. In the insert function tab you will see all functions.
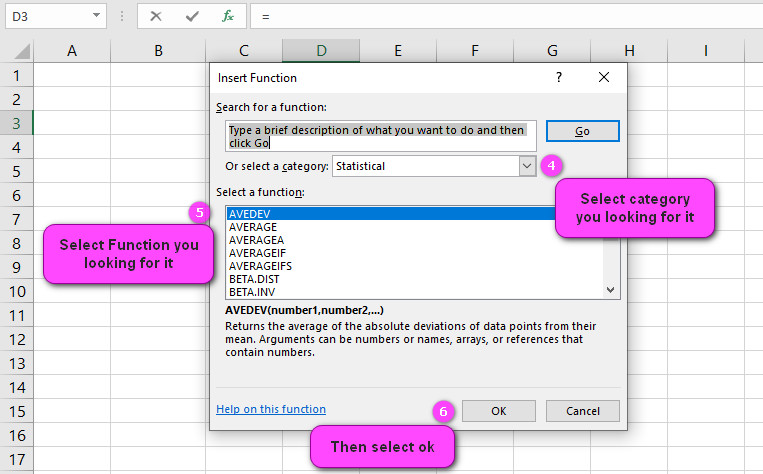
4. Select STATISTICAL category.
5. Select LOGNORM.DIST function.
6. Then select ok.
7. In the function arguments Tab you will see LOGNORM.DIST function.
8. X is the value at which to evaluate the function, a positive number.
9. Mean is the mean of ln(x).
10. Standard_dev is the standard deviation of ln(x), a positive number.
11. Cumulative is a logical value: for the cumulative distribution function, use TRUE; for
the probability density function, use FALSE.
12. You will see the results in the formula result section.
What is the syntax of the LOGNORM.DIST function in Excel?
The LOGNORM.DIST function in Excel is used to calculate the cumulative distribution function (CDF) of a lognormal distribution. The syntax for this function is as follows:
=LOGNORM.DIST(x, mean, standard_dev, cumulative)
where:
- x: This is the value at which you want to evaluate the CDF.
- mean: This is the mean of the logarithm of the distribution.
- standard_dev: This is the standard deviation of the logarithm of the distribution.
- cumulative: This is a logical value that specifies whether to return the cumulative distribution or the probability density function (PDF). If cumulative is TRUE or omitted, then the function returns the cumulative distribution. If cumulative is FALSE, then the function returns the PDF.
Here are some examples of how to use the LOGNORM.DIST function in Excel:
Example 1: Find the cumulative distribution function of a lognormal distribution with mean 2 and standard deviation 0.5 at x=4.
=LOGNORM.DIST(4, 2, 0.5, TRUE)
This will return a value of approximately 0.69146246.
Example 2: Find the probability density function of a lognormal distribution with mean 1 and standard deviation 0.2 at x=2.
=LOGNORM.DIST(2, 1, 0.2, FALSE)
This will return a value of approximately 0.05483362.
Note that the LOGNORM.DIST function assumes that the logarithm of the data follows a normal distribution.
Therefore, this function is often used to model data that are positively skewed and have many small values and a few very large values.
What does the LOGNORM.DIST function do?
The LOGNORM.DIST function is a statistical function in Microsoft Excel and Google Sheets that calculates the cumulative distribution function (CDF) of a log-normal distribution.
The log-normal distribution is a probability distribution of a random variable whose logarithm is normally distributed.
Here’s an example of how to use the LOGNORM.DIST function:
Suppose we have a log-normally distributed set of data with a mean of 10 and a standard deviation of 1. We want to find the probability that a randomly selected value from this distribution will be less than or equal to 12. To do this, we can use the following formula:
=LOGNORM.DIST(12,10,1,TRUE)
The result of this calculation is approximately 0.9088, which means there is a 90.88% chance that a randomly selected value from this distribution will be less than or equal to 12.
Alternatively, if we wanted to find the probability density function value for x = 12, we would use the following formula:
=LOGNORM.DIST(12,10,1,FALSE)
This would give us a result of approximately 0.0337, which is the probability density value for x = 12.
How do I use the LOGNORM.DIST function to calculate probabilities in Excel?
The LOGNORM.DIST function in Excel is used to calculate the cumulative distribution function (CDF) of a log-normal distribution.
The function returns the probability that a random variable from a log-normal distribution falls between two specified values.
The syntax for the LOGNORM.DIST function is as follows:
=LOGNORM.DIST(X, Mean, Standard_dev, Cumulative)
where: X = the value at which you want to evaluate the distribution Mean = the arithmetic mean of the logarithm of the distribution Standard_dev = the standard deviation of the logarithm of the distribution Cumulative = a logical value that determines the form of the function’s output.
If Cumulative is TRUE, then LOGNORM.DIST returns the cumulative distribution function; if FALSE, it returns the probability density function.
Here is an example of how to use the LOGNORM.DIST function in Excel:
Suppose we have a log-normal distribution with a mean of 2 and a standard deviation of 0.5.
We want to calculate the probability that a random variable from this distribution falls between 3 and 4.
To do this, we can use the following formula:
=LOGNORM.DIST(4, 2, 0.5, TRUE) – LOGNORM.DIST(3, 2, 0.5, TRUE)
This formula calculates the cumulative distribution function for X = 4 and subtracts the cumulative distribution function for X = 3. The result is the probability that a random variable from the distribution falls between 3 and 4.
If we enter this formula into cell A1 of an Excel spreadsheet, we get the answer 0.0861, which means there is an 8.61% chance that a random variable from the distribution falls between 3 and 4.
What are the arguments required by the LOGNORM.DIST function?
The LOGNORM.DIST function in Excel is used to calculate the cumulative distribution function (CDF) or the probability density function (PDF) of a lognormal random variable.
There are four arguments required by the LOGNORM.DIST function, which are as follows:
- X: This is the value for which we want to calculate the distribution function. It must be a positive number.
- Mean: This is the mean of the logarithm of the random variable. It can be any real number.
- Standard_dev: This is the standard deviation of the logarithm of the random variable. It must be a positive number.
- Cumulative: This is a logical value that determines whether we want to calculate the CDF or PDF. If it is set to TRUE or omitted, the function returns the CDF. If it is set to FALSE, the function returns the PDF.
Here’s an example of how to use the LOGNORM.DIST function to calculate the probability that a stock will be worth at least $100 in one year, given that it has a lognormal distribution with a mean annual return of 10% and an annualized volatility of 20%:
=LOGNORM.DIST(100, LN(1+0.1), 0.2, TRUE)
In this example, we have set X to 100, which represents the target price. We have used the LN function to convert the mean annual return of 10% to its logarithmic equivalent (i.e., 0.09531).
We have set the standard deviation to 0.2, which represents the annualized volatility.
Finally, we have set the Cumulative argument to TRUE, which means we want to calculate the probability that the stock will be worth at least $100 in one year.
The result of this function is 0.4519, which means there is a 45.19% chance that the stock will be worth at least $100 in one year.
How do I specify the mean and standard deviation for the LOGNORM.DIST function?
The LOGNORM.DIST function in Excel is used to calculate the cumulative distribution function or probability density function of a lognormal distribution.
The lognormal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed.
To specify the mean and standard deviation for the LOGNORM.DIST function, you need to provide two arguments:
- X: This is the value at which you want to evaluate the distribution.
- Mean: This represents the mean of the natural logarithm of the random variable.
- Standard_dev: This represents the standard deviation of the natural logarithm of the random variable.
The formula for the cumulative distribution function (CDF) in Excel is:
=LOGNORM.DIST(X, Mean, Standard_dev, Cumulative)
Where: X – The value at which you want to evaluate the distribution. Mean – The mean of the natural logarithm of the random variable.
Standard_dev – The standard deviation of the natural logarithm of the random variable. Cumulative – A logical value that determines the form of the function.
If Cumulative is TRUE, then LOGNORM.DIST returns the CDF; if FALSE, the PDF.
Let’s take an example to understand this better:
Suppose you have a dataset with the following values: 1, 2, 3, 4, 5. You want to calculate the probability that a randomly chosen number from the set is less than or equal to 3.
For this, you can use the LOGNORM.DIST function with the following inputs:
X = 3 Mean = 1.6 (the mean of ln(1), ln(2), ln(3), ln(4), ln(5)) Standard_dev = 0.69 (the standard deviation of ln(1), ln(2), ln(3), ln(4), ln(5)).
The formula would be:
=LOGNORM.DIST(3, 1.6, 0.69, TRUE).
This will give you the probability that a randomly chosen number from the set is less than or equal to 3.
Can I use the LOGNORM.DIST function to generate random numbers in Excel?
you can use the LOGNORM.DIST function in Excel to generate random numbers. The LOGNORM.DIST function returns the cumulative distribution function (CDF) of a log-normal distribution.
The CDF represents the probability that a random variable is less than or equal to a certain value.
To generate random numbers using the LOGNORM.DIST function, you can use the inverse of the CDF, which is called the percent point function (PPF) or quantile function.
The PPF takes a probability value between 0 and 1 as input and returns the corresponding value from the distribution.
Here is an example of how to use the LOGNORM.DIST function to generate random numbers in Excel:
Suppose you want to generate 10 random numbers from a log-normal distribution with a mean of 5 and a standard deviation of 1. To do this, you can follow these steps:
- In cell A1, enter “=RAND()” without quotes. This will generate a random number between 0 and 1.
- In cell B1, enter “=LOGNORM.INV(A1,5,1)” without quotes. This will convert the random number generated in step 1 into a value from the log-normal distribution with a mean of 5 and a standard deviation of 1.
- Copy cell B1 and paste it into cells B2:B10. This will generate 10 random numbers from the log-normal distribution with a mean of 5 and a standard deviation of 1.
The resulting values in cells B1:B10 will be different each time you recalculate the worksheet due to the use of the RAND() function.
Note that the LOGNORM.DIST function may not be available in older versions of Excel, but it is available in Excel 2010 and later versions.
What is the difference between the LOGNORM.DIST and NORM.DIST functions in Excel?
The LOGNORM.DIST and NORM.DIST functions in Excel are both used to calculate probabilities for a normal distribution, but they differ in the way they interpret data.
The NORM.DIST function calculates the probability that a given value falls within a specified range of a normal distribution with a specified mean and standard deviation. Its syntax is:
=NORM.DIST(x, mean, standard_dev, cumulative)
For example, if you want to determine the probability that a randomly selected person’s height is between 170 cm and 180 cm, given that the population mean height is 165 cm with a standard deviation of 10 cm, you could use the formula:
=NORM.DIST(180, 165, 10, TRUE) – NORM.DIST(170, 165, 10, TRUE)
This would return the probability that a person’s height falls within this range.
On the other hand, the LOGNORM.DIST function calculates the probability that a random variable has a value less than or equal to a specified value, where the logarithm of the random variable follows a normal distribution. Its syntax is:
=LOGNORM.DIST(x, mean, standard_dev, cumulative)
For example, if you want to determine the probability that a stock price will be less than $50 per share at the end of the year, given that the average rate of return on the stock is 8% with a standard deviation of 12%, you could use the formula:
=LOGNORM.DIST(50, 0.08, 0.12, TRUE)
This would return the probability that the logarithm of the stock price at the end of the year follows a normal distribution with a mean of 8% and a standard deviation of 12%, and is less than or equal to the logarithm of $50.
In summary, the NORM.DIST function calculates the probability of a value falling within a range in a normal distribution, while the LOGNORM.DIST function calculates the probability of a value being less than or equal to a specified value in a lognormal distribution.
Can the LOGNORM.DIST function be used for both positive and negative values?
The LOGNORM.DIST function in Excel can only be used for positive values. This is because the function is designed to calculate the probability distribution of a logarithmic normal variable, which must have a positive value.
The LOGNORM.DIST function returns the cumulative distribution function (CDF) of a logarithmic normal distribution. The syntax of the function is as follows:
=LOGNORM.DIST(x, mean, standard_dev, cumulative)
Here’s an example of how to use the LOGNORM.DIST function to calculate the cumulative distribution function for a set of positive values:
Suppose we have a set of data containing the number of hours it takes for a group of workers to complete a task.
We want to calculate the probability of a worker completing the task in less than or equal to 5 hours, given that the mean time taken is 4 hours and the standard deviation is 1 hour.
We can use the LOGNORM.DIST function as follows:
=LOGNORM.DIST(5, 4, 1, TRUE)
This will return a value of approximately 0.8413, indicating that there is an 84.13% chance that a worker will complete the task in less than or equal to 5 hours.
However, if we have negative values in our data, we cannot use the LOGNORM.DIST function as it is only applicable for positive values.
For negative values, we may need to use a different distribution function that is appropriate for our data.
What are some practical applications of the LOGNORM.DIST function in Excel?
The LOGNORM.DIST function in Excel is used to calculate the cumulative probability of a random variable that follows a lognormal distribution.
The lognormal distribution is a continuous probability distribution of a random variable whose logarithm is normally distributed.
One practical application of the LOGNORM.DIST function is in financial modeling, where it is often used to model the returns of an investment over time.
For example, suppose you have historical data on the daily returns of a stock and you want to calculate the probability that the stock will return more than a certain amount over a given period of time.
You can use LOGNORM.DIST to calculate this probability.
Here’s an example:
Suppose you have a set of data representing the daily returns of a stock over the past year.
You want to know the probability that the stock will return more than 3% over the next month. You can use LOGNORM.DIST to calculate this probability as follows:
Copy Code=1-LOGNORM.DIST(0.03/30, AVERAGE(Returns), STDEV(Returns), TRUE)
In this formula, 0.03/30 represents the daily return required to achieve a 3% return over the course of a month, AVERAGE(Returns) represents the average daily return over the past year, STDEV(Returns) represents the standard deviation of the daily returns over the past year, and TRUE indicates that we want to calculate the cumulative probability.
Another practical application of the LOGNORM.DIST function is in engineering, where it is often used to model the distribution of particle sizes in a sample.
For example, suppose you have a sample of particles and you want to know the probability that a particle will have a certain size. You can use LOGNORM.DIST to calculate this probability.
Here’s an example:
Suppose you have a sample of particles and you want to know the probability that a particle will be between 5 and 10 microns in size. You can use LOGNORM.DIST to calculate this probability as follows:
Copy Code=LOGNORM.DIST(10, 7, 1.5, TRUE) - LOGNORM.DIST(5, 7, 1.5, TRUE)
In this formula, 10 represents the upper bound of the desired particle size range, 7 represents the mean particle size, 1.5 represents the standard deviation of the particle sizes, and TRUE indicates that we want to calculate the cumulative probability.
We subtract this value from the cumulative probability at the lower bound of the desired range to obtain the probability of a particle being in the desired range.
Are there any limitations or issues with using the LOGNORM.DIST function in Excel?
there are some limitations and issues with using the LOGNORM.DIST function in Excel that you should be aware of.
The LOGNORM.DIST function is used to calculate the cumulative distribution function (CDF) or probability density function (PDF) of a log-normal distribution.
It takes four arguments: x (the value at which to evaluate the function), mean (the mean of the ln(x) values), standard_dev (the standard deviation of the ln(x) values), and cumulative (a logical value that determines the form of the function).
Here are some limitations and issues to consider when using the LOGNORM.DIST function:
- The function assumes a log-normal distribution, which may not accurately represent your data. If your data follows a different distribution, the results of the function may not be meaningful.
- The function may return unexpected results if any of the input values are negative or zero. This is because the logarithm function is undefined for non-positive numbers.
- The function may return misleading results if the mean and/or standard deviation parameters are not chosen appropriately for the data. For example, if the data has a long tail, the use of a large standard deviation value may result in an overestimate of the probability of extreme events.
- Depending on the application, you may need to use the LOGNORM.INV function instead of LOGNORM.DIST. LOGNORM.INV is used to calculate the inverse of the CDF, which gives you the value of x that corresponds to a given probability. This can be useful for risk analysis or simulation modeling.
Here’s an example of how to use the LOGNORM.DIST function in Excel:
Suppose you have a set of data representing the values of stocks in a particular industry. You want to use the log-normal distribution to model the likelihood of certain outcomes.
You could use the following formula to calculate the cumulative distribution function for a value of x = 100, given a mean of 5 and a standard deviation of 1:
=LOGNORM.DIST(100, 5, 1, TRUE)
This would return the probability that a randomly chosen stock in the industry is worth less than or equal to $100. You could also use FALSE for the cumulative argument to get the PDF value instead.
In summary, while the LOGNORM.DIST function can be useful for modeling log-normal distributions in Excel, it has some limitations and issues that should be considered when interpreting its results.
Examples of LOGNORM.DIST function in Excel
here are 10 examples of the LOGNORM.dist function in Excel:
- =LOGNORM.DIST(100,50,10,FALSE)
- Calculates the probability density function for the lognormal distribution with a mean of 50 and a standard deviation of 10 at x=100.
- =LOGNORM.DIST(0.5,1,0.2,TRUE)
- Calculates the cumulative distribution function for the lognormal distribution with a mean of 1 and a standard deviation of 0.2 at x=0.5.
- =LOGNORM.DIST(75,80,12,FALSE)
- Calculates the density function for the lognormal distribution with a mean of 80 and a standard deviation of 12 at x=75.
- =LOGNORM.DIST(5000,10000,2000,TRUE)
- Calculates the cumulative distribution function for the lognormal distribution with a mean of 10000 and a standard deviation of 2000 at x=5000.
- =LOGNORM.DIST(2,1,0.5,FALSE)
- Calculates the probability density function for the lognormal distribution with a mean of 1 and a standard deviation of 0.5 at x=2.
- =LOGNORM.DIST(0.8,0.7,0.05,TRUE)
- Calculates the cumulative distribution function for the lognormal distribution with a mean of 0.7 and a standard deviation of 0.05 at x=0.8.
- =LOGNORM.DIST(150,120,30,FALSE)
- Calculates the density function for the lognormal distribution with a mean of 120 and a standard deviation of 30 at x=150.
- =LOGNORM.DIST(0.25,0.2,0.05,TRUE)
- Calculates the cumulative distribution function for the lognormal distribution with a mean of 0.2 and a standard deviation of 0.05 at x=0.25.
- =LOGNORM.DIST(10,8,2,FALSE)
- Calculates the probability density function for the lognormal distribution with a mean of 8 and a standard deviation of 2 at x=10.
- =LOGNORM.DIST(200,150,50,TRUE)
- Calculates the cumulative distribution function for the lognormal distribution with a mean of 150 and a standard deviation of 50 at x=200.